| Публикации: | АСУТП | Теория и технология | Научные работы | Главная |
МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ УССР
ДОНЕЦКИЙ ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ
Храпко Сергей Александрович
УДК 669.187:541.123
Термодинамическая модель системы металл-шлак для АСУ и машинных экспериментов по оптимизации технологии сталеплавильного процесса
Специальность 05.16.02 - "Металлургия чёрных металлов"
Автореферат диссертации на соискание учёной степени кандидата технических наук
Научный руководитель - доктор технических наук, профессор Пономаренко А.Г.
Официальные оппоненты: доктор технических наук, профессор Михайлов Г.Г., кандидат технических наук, старший научный сотрудник Тогобицкая Д.Н.
Ведущее предприятие - Московский институт стали и сплавов.
Актуальность работы. Одним из основных резервов совершенствования качества продукции, повышения экономической эффективности и улучшения экологических показателей производства является широкое использование ВТ для управления, исследований, прогнозирования и т.д.
Изучение на ЭВМ сложных физико-химических моделей многокомпонентных систем представляет наибольший интерес в научных и практических приложениях химической термодинамики как новое, перспективное средство исследований. Многие дорогостоящие экспериментальные и опытно-технологических работы сейчас могут быть успешно, гораздо быстрее, и с минимальными затратами выполнены физико-химическим моделированием на компьютерах. Существует также множество задач, единственным способом решения которых является физико-химическое моделирование на ЭВМ.
Всякое управление связано с необходимостью предсказания, предвидения результатов тех или иных возможных воздействий на технологический процесс. В случае таких сложных технологий, какой является металлургическая плавка, задача предвидения является узловой, сосредоточивающей в себе наиболее важные проблемы, лимитирующие развитие таких систем управления.
Настоящая работа посвящена развитию таких моделей для имитации процессов выплавки стали и использованию их с целью решения реальных технологических задач.
Цель работы. На основе экспериментального и теоретического анализа распределения элементов между фазами разработать формализованную модель системы металл-шлак-газ с участием элементов постоянной и переменной валентности для автоматизированных систем управления и проведения машинных экспериментов по оптимизации технологии сталеплавильного процесса.
Идея работы заключается в использовании строгого аппарата классической термодинамики и последних разработок в области уравнений состояния для построения формализованной модели системы металл-шлак и численного моделирования на ее основе реальных металлургических процессов.
Научная новизна. Работа включает следующие новые научные результаты и положения, выносимые на защиту:
Обоснованность и достоверность научных результатов и выводов, приведенных в диссертации, подтверждается их последовательным математическим обоснованием и сопоставлением с экспериментальными и технологическими данными. Адекватность уравнений, полученных в работе, подтверждается методами математической статистики. Машинные эксперименты, проведенные в работе, имеют удовлетворительную воспроизводимость, их результаты согласуются с имеющимися литературными и производственными данными.
Научная значимость. Результаты, представленные в работе, расширяют возможности применения математического аппарата термодинамики и являются шагом в совершенствовании расчетов прогнозирующего характера. Разработанная в виде алгоритмов и программ термодинамическая модель сталеплавильного процесса позволяет оценивать химические составы и количества металла, шлака и газообразных продуктов по ходу плавки с точностью, достаточной для технологических целей, что открывает новые возможности в проектировании АСУ ТП.
Практическое значение работы подтверждается успешным применением созданной модели системы металл-шлак-газ в МИСиС, ИЧМ, НИИМ, ДМетИ, ХМИ АН Каз.ССР, ЧМК при проведении научно-исследовательских работ и в учебном процессе. Применение указанной разработки для машинных экспериментов и термодинамического анализа сталеплавильных и ферросплавных процессов позволяет сократить количество сложных заводских экспериментов при оптимизации технологических параметров процессов. Разработанный алгоритм принят к внедрению в качестве основного варианта АСУ верхнего уровня агрегата "печь-ковш" в проекте реконструкции ЭСПЦ-2 ЧМК.
Апробация работы. Материалы диссертации доложены и обсуждены на конференциях и семинарах: на научно-технической конференции "Научно-технический прогресс в производстве стали и ферросплавов" (Челябинск, 1988); на Всесоюзном совещании "Базы физико-химических и технологических данных для оптимизации металлургических технологий" (Днепропетровск, 1988); на научном семинаре "Аналитическое представление концентрационной зависимости термодинамических функций в расплавленных металлических и солевых системах. Математические методы и физические модели" (Ленинград, 1988); на Всесоюзной конференции "Создание и совершенствование энергосберегающих технологий в пирометаллургии" (Караганда, 1988); на VI Всесоюзной школе-семинаре "Применение математических методов для описания и изучения физико-химических равновесий" (Новосибирск, 1989); на I советско-чехословацком симпозиуме по теории металлургических процессов (Москва, 1989); на II Всесоюзном совещании "Применение ЭВМ в научных исследованиях и разработках" (Днепропетровск, 1989).
Публикации. Основные результаты диссертации изложены в десяти печатных работах.
Объем работы. Диссертация изложена на 115 страницах машинописного текста и содержит введение, 5 глав, заключение, 8 рисунков, 10 таблиц, список использованной литературы из 105 наименований и приложения.
В первой главе проанализировано состояние исследуемого вопроса. Конечная цель плавки стали в общем случае сводится к получению заданной массы жидкой стали с требуемыми химическим составом и температурой. Получение заданного химического состава готовой стали относится к числу сложных задач управления, поскольку она связана с протеканием сложных физико-химических процессов, часть из которых трудно управляема или вовсе неуправляема.
Во всех своих приложениях математика оперирует моделями рассматриваемых объектов. Модель - это уравнение или система уравнений, связывающих основные, с точки зрения решаемой задачи, свойства реального объекта. Модель плавки - это иерархическая система уравнений трех уровней: модель фазы - модель системы металл-шлак-газ - модель плавки.
Можно выделить два крайних способа построения таких моделей: статистические ("чёрный ящик") и теоретические (детерминированные), не требующие подгоночных коэффициентов, определяемых из массива опытных данных.
Наиболее общий путь для сложных объектов - "черный ящик" (эмпирические модели) - используются в качестве первой ступени исследования, когда полностью отсутствует или игнорируется информация о внутренних взаимосвязях параметров объекта. Применение статистических моделей оправдано при оптимизации характеристик конкретных технологических процессов в условиях, близких к существующим, а моделирование новых условий (экстраполяция) в большинстве случаев невозможно.
Обычно используемые модели имеют некоторую теоретическую основу со статистическим определением параметров, которые не могут быть вычислены теоретически, т.е. часть связей определяется теоретическими соотношениями. Теоретические модели короче и информативнее, т.е. производят более эффективную свёртку информации, применимы к широкому кругу технологий, рассматриваемых как частные случаи. Чем больше доля теоретических уравнений, тем более универсальна модель и выше ее прогностические возможности. Теоретические модели устойчивы по отношению к случайной информации, позволяют делать априорные оценки при полном отсутствии экспериментальных данных.
При рассмотрении теоретических моделей часто противопоставляют, например, термодинамические и кинетические модели на том основании, что все реальные процессы неравновесны и не могут быть описаны в терминах термодинамики, основанной на рассмотрении равновесных состояний. В действительности кинетическая модель не может быть полноценной, если она не опирается на термодинамику. Термодинамика определяет необходимые для кинетических расчетов теоретические пределы и направление протекания процесса, движущие силы, а в ряде случаев и сопротивления (например, условия зарождения новых фаз в виде пузырьков, дисперсных включений), поэтому существенная свёртка модели, основанной на кинетических закономерностях, возможна лишь при использовании термодинамики. Термодинамика позволяет раскрыть смысл многих коэффициентов таких моделей, выразив их через фундаментальные теоретические зависимости и константы. Взаимодействие потоков, их предельное смещение наиболее обоснованно определяет термодинамика необратимых процессов. Чисто кинетическая модель отличается от "черного ящика" лишь видом уравнений связи, коэффициенты которых, как и в "черном ящике" находятся из массива опытных данных, относящихся к конкретному процессу и даже агрегату. Поэтому она не может быть использована для априорных количественных оценок. Принципиальный момент состоит в том, что термодинамика позволяет построить работоспособную общую модель и делать априорные количественные оценки без адаптации к конкретному процессу (т.е. без подбора констант по опытным данным).
Известные в настоящее время модели наряду с теоретически обоснованными зависимостями включают значительное количество эмпирических связей и коэффициентов. В обзоре главное внимание уделено термодинамическим детерминированным моделям многофазных систем и выбору термодинамических функций неидеальных растворов сложного состава.
Детерминированные термодинамические модели системы металл-шлак включают в себя законы сохранения (уравнения материального баланса, электронейтральности, и др.) и условия термодинамического равновесия, определяемые по минимуму свободной энергии (Гиббса или Гельмгольца) или по максимуму энтропии. В соответствии с этим модель плавки представляет собой сложную систему уравнений, решение которой применительно к условиям реальных процессов встречает определенные трудности. Поэтому известные в настоящее время модели плавки громоздки, неуниверсальны, используют большое число упрощающих предположений и не доведены до реальных технологических расчетов. Кроме того, многие из них не учитывают неидеальность конденсированных фаз, что дополнительно ограничивает их применимость.
Отмечено, что при термодинамическом моделировании металлургических равновесий выбор функций состав-свойство (модели уравнений состояния) конденсированных фаз определяет наиболее важные результаты моделирования сталеплавильных процессов.
Строгая теория жидкостей (и вообще конденсированных фаз) в настоящее время позволяет получить лишь качественное описание термодинамических свойств простейших систем. Широкое распространение в расчетах получили упрощенные методы, при которых заранее принимаются допущения о структуре расплава и характере взаимодействия его частиц и учитывается только конфигурационная часть энтропии. Существует также и большая группа моделей, в которых выражения для термодинамических свойств расплава получаются формальным разложением в полиномиальный ряд и последующим определением коэффициентов методами математической статистики по массивам экспериментальных данных. Рассмотрены и проанализированы модели, наиболее часто используемые для описания термодинамических свойств металлических и шлаковых расплавов. На основании анализа состояния вопроса сформулированы задачи исследования:
Создание моделей фаз в задачи исследования не входило.
Вторая глава посвящена выбору моделей уравнений состояния для металлической и шлаковой фаз из имеющихся в литературе на основе соотношений общей термодинамики. В металлургической литературе этот вопрос известен как проблема активностей.
Термодинамика постулирует сам факт существования уравнения состояния, например, в виде
| | (1) |
где | G | – | интегральная функция. При описании химических равновесий используются производные функции (1). |
Во всех практических расчетах используют те или иные конкретные выражения - модели уравнения состояния, которые лишь приближенно характеризуют фазу. Модель фазы (1) является первой ступенью в иерархической системе моделей: модель фазы - модель системы металл-шлак-газ - модель плавки.
Модели конденсированных фаз, несмотря на многочисленные разработки, являются наиболее уязвимым местом всех термодинамических расчетов реальных систем. Известные модели металлических и шлаковых растворов не всегда обеспечены численными значениями параметров, не определены границы их применимости, что часто затрудняет их использование даже для грубых априорных оценок.
Модели фаз, независимо от способа их получения, являются аппроксимирующими функциями, что налагает на них ряд специфических требований с точки зрения возможности и корректности их математических преобразований. Кроме того, необходимо, чтобы каждое из используемых уравнений для отдельных фаз удовлетворяло ряду общих требований термодинамики растворов (фундаментальное уравнение Гиббса, предельные законы и др.). И, наконец, поскольку эти уравнения используются для описания системы фаз, на них должны распространяться дополнительные требования, налагаемые этой системой, такие как выбор компонентов, устойчивость во всей области изменения параметров и др.
Основным требованием к модели является ее адекватность реальному объекту, которая достигается выбором вида функций и оптимизацией входящих в них коэффициентов. Математические преобразования аппроксимирующих функций, в частности их дифференцирование, может приводить к катастрофической утрате адекватности (так называемые некорректно поставленные задачи). По этой причине, например, не всегда корректны оценки активностей по параметрам моделей, определяемым из интегральной энтальпии. Поскольку выбранные функции для описания термодинамических свойств расплавов должны удовлетворять фундаментальному уравнению Гиббса (или уравнению Гиббса-Дюгема в частном случае постоянства температуры и давления), то модель фазы должна представлять собой одну из характеристических функций состояния, т.е. интегральное свойство фазы. Кроме того, уравнение должно быть аналитическим, непрерывным и дифференцируемым (для анализа устойчивости фазы как минимум дважды) во всей области существования фазы.
Если модель фазы представлена уравнениями для парциальных характеристик (например, разложение Вагнера), то должны соблюдаться условия совместности (интегрируемости), которые гарантируют, что дифференцирование двух или более уравнений ![]() приводит к совпадению производных высшего порядка от функции Φ:
приводит к совпадению производных высшего порядка от функции Φ:
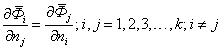 | (2) |
Если условия совместности (2) не выполняются при любых значениях независимых параметров в области определения фазы, то это говорит о внутренней противоречивости модели и приводит, например, к нарушению уравнения Гиббса-Дюгема.
При построении формализованных моделей фаз важно минимизировать количество параметров модели при сохранении удовлетворительной точности аппроксимации свойств. Этого можно достичь выбором уравнений с использованием атомных параметров ai, взамен, например, парных aij, при этом каждому компоненту раствора в простейшем случае соответствует один постоянный коэффициент, не зависящий от состава и типа раствора. Для формализации модели требуется также идентичность расчетных формул для всех компонентов фазы.
В работе сформулированы и обоснованы предельные условия для уравнений состояния в виде дифференциальных формулировок законов Рауля и Генри (в терминах активности):
 | (3) |
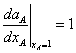 | (4) |
где | γ0B | – | коэффициент активности компонента B при бесконечном разбавлении в компоненте A – конечная величина, не равная нулю; |
| ai и xi | – | активность и мольная доля компонента i в растворе. |
Отмечено, что термодинамическая устойчивость не относится к числу общих требований к уравнению состояния, а лишь подтверждает непротиворечивость полученного решения для системы фаз.
При рассмотрении температурной зависимости термодинамических функций необходимо учитывать экспоненциальную зависимость отклонений от идеальности при повышении температуры, и третий постулат термодинамики о нулевом значении энтропии при абсолютном нуле, т.е. снижение энтропии при понижении температуры.
На основе рассмотренных требований были проанализированы известные модели фаз. В настоящее время широко используемым методом расчета активностей в металлической фазе, обеспеченным численными значениями параметров для большинства используемых в металлургии стали элементов является метод Вагнера:
| (5) |
Однако главный недостаток разложения Вагнера, ограничивающий его использование в области концентрированных растворов состоит в том, что он дает принципиально неверный ход активности в области высоких концентраций (не согласуется с уравнением Гиббса-Дюгема и не выходит на требуемый им закон Рауля в точке чистого растворенного вещества). Представление опытных данных в терминах разложения Вагнера в этой области теряет всякую основу и особо опасно для экстраполяции. Эта особенность разложения Вагнера связана с тем, что аппроксимирующая функция является точной лишь в одном конце концентрационного интервала.
Кроме того, при использовании разложения Вагнера не выполняется условие совместности (2). Альтернативой методу Вагнера является теория субрегулярных растворов (ТСР), позволяющая описывать экспериментальные данные с такой же точностью и содержащая аналогичное количество коэффициентов:
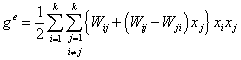 | (6) |
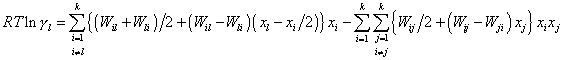 | (7) |
ТСР удовлетворяет всем перечисленным выше требованиям к уравнению состояния, однако не обеспечена численными значениями параметров. Тем не менее, используя формулы ТСР можно "утилизировать" имеющиеся данные по параметрам взаимодействия для получения численных значений входящих в выражения (6)-(7) параметров этой модели. Рассматривая выражение (7) для бинарной системы l - r и тройной l - m - r, где r - растворитель, можно перейти к параметрам взаимодействия Вагнера, продифференцировав (7) по мольной доле соответствующего компонента (с учетом dxr / dxi = -1):
| (8) |
| (9) |
| (10) |
Полученные таким образом параметры ТСР позволяют описывать металлические растворы во всем диапазоне составов, причем в области малых концентраций примесей уравнение (7) будет давать результаты, совпадающие с формулой Вагнера, а при повышенных концентрациях примесей и в области чистых растворенных веществ формулу (7) можно более обоснованно использовать для оценочных расчетов коэффициентов активности при отсутствии экспериментальных данных.
Для расчёта активностей в шлаковой фазе принята модель А.Г. Пономаренко (МКЭ), как удовлетворяющая изложенным выше требованиям. Выражение для химического потенциала элемента в оксидной фазе μ(i) имеет вид
| (11) |
Величина γ(i) определяется выражением
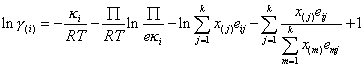 | (12) |
где | x(i) | – | мольная доля; |
| k | – | число атомов разного сорта; | |
| – | фактор Больцмана; | ||
| – | энергия смешения; | ||
| κi | – | параметр модели, атомный потенциал. |
Важными характеристиками указанного метода являются его общность, формальность и возможность использования для фаз любого состава.
В третьей главе описывается построение модели следующего уровня - термодинамической модели системы металл-шлак-газ. В процессе металлургического передела участвует множество фаз, такие как металл, шлак, газовая фаза, футеровка, неметаллические включения (НВ) и др. Все они взаимосвязаны и оказывают влияние друг на друга, однако в сталеплавильных процессах основная масса реагирующих веществ сосредоточена в металлической и шлаковой фазах, поэтому термодинамической основой представленной модели является равновесие системы металл-шлак, а состав газовой и других фаз определяется дополнительным расчетом с последующей коррекцией перераспределения масс между всеми фазами. В базовом варианте модели газовая фаза полагается состоящей только из CO и CO2. Указанная система считалась закрытой, влияние футеровки учитывалось введением в качестве исходного материала состава и количества расходуемых заправочных материалов.
В общем виде модель (система уравнений) состоит из двух элементов. Первый исходит из условия равновесия Гиббса
| (13) |
или в терминах химических потенциалов для системы металл-шлак-газ
| (14) |
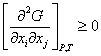 | (15) |
В выражения (13)-(15) входят рассмотренные ранее модели фаз (1). В качестве базовых были использованы формулы ТСР и МКЭ, однако описываемый алгоритм допускает их замену другими уравнениями состояния.
Вторым элементом являются законы сохранения (уравнения материального баланса и условие электронейтральности):
| (16) |
| (17) |
где | α | – | индекс фазы; |
| i | – | индекс компонента; | |
| mαi, Mi, ναi | – | масса, молекулярная масса и валентность компонента i в фазе α. |
Выразив химические потенциалы через активности и учитывая наличие CO и CO2 в газовой фазе получим следующую систему уравнений:
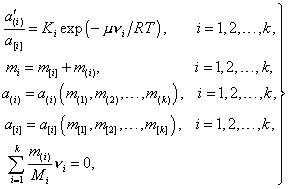 | (18) |
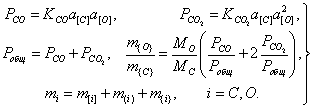 | (19) |
Если производится расчет без учета удаления углерода и кислорода в газовую фазу, то решается система уравнений (18) методом рекуррентных итераций или методом Ньютона. В результате получаем составы и количества металла и шлака. По окончании расчета определяются парциальные давления оксидов углерода и общее равновесное давление в газовой фазе. Если полученное значение превышает заданное атмосферное давление, то система уравнений (18) дополняется уравнениями (19), и снова производится ее решение. В этом случае кроме составов и количеств металла и шлака определяются состав и количество равновесной газовой фазы при заданном постоянном внешнем давлении, а также парциальные давления окиси и двуокиси углерода.
При необходимости учёт неравновесности производится обработкой ограниченного количества производственных данных с коррекцией заложенных в модель констант равновесия или определением поправок. Полученные таким образом константы или поправки характеризуют частный массив данных и включают в себя особенности агрегата, процесса, интенсивность перемешивания ванны и протекания реакций, неучтённое воздействие футеровки и другие факторы. В модели плавки предусмотрена возможность постоянной корректировки этих констант по имеющимся экспериментальным данным, чем учитываются текущие изменения состояния агрегата и других условий.
В производственных условиях становится острым вопрос использования неполных данных и получения из них всей необходимой информации. При этом используется то обстоятельство, что константы (в терминах МКЭ) взаимосвязаны:
| (20) |
| (21) |
Константы распределения в этом случае находятся решением избыточной системы линейных уравнений вида (20) и (21):
| (22) |
где | K | – | вектор логарифмов искомых констант; |
| X | – | матрица коэффициентов при константах в левых частях уравнений (20)-(21); | |
| F | – | вектор значений в правых частях этих уравнений. |
Возможны любые варианты выбора базовых констант, однако в предлагаемой модели используются константы образования оксидов, имеющиеся данные о которых отличаются наибольшей надежностью, что и определило их выбор. Такой выбор позволяет так же утилизировать информацию в терминах традиционных констант равновесия ЗДМ, имеющуюся в металлургической литературе.
Для многих моделей фаз приводятся численные значения коэффициентов, входящих в эти модели, без указания границ их применимости по составу фазы. Для решения вопроса о применимости использованных в расчете моделей использован критерий устойчивости фазы к бесконечно малым изменениям состояния
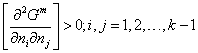 | (23) |
который позволяет отделить устойчивые состояния фазы (стабильные и метастабильные) от полностью неустойчивых (лабильных).
При нарушении положительной определенности матрицы вторых частных производных энергии Гиббса фазы по числам молей компонентов можно обоснованно утверждать, что при указанном составе фазы либо должно произойти ее расслаивание, либо модель неприменима в этом диапазоне концентраций компонентов. В любом случае результаты расчета не будут соответствовать действительности и необходимо заменить используемую модель на более общую, описывающую больший диапазон составов фазы.
В четвертой главе дается подробное описание алгоритма решения задачи расчета равновесных составов металла, шлака и газа.
В пятой главе приводятся примеры проверки адекватности модели. Для выяснения работоспособности модели и точности получаемого решения были проведены многочисленные машинные эксперименты, имитирующие выплавку стали и ферросплавов в различных агрегатах. В табл.1 приведены результаты расчета состава металла при выплавке стали ШХ15 в ЭСПЦ-2 ЧМК. При этом по заводским картам плавок задавались количества шихтовых материалов (лом, чугун, шлакообразующие, окислители, легирующие и восстановители) и рассчитывались составы и количества металла и шлака.
Таблица 1. Состав металла промышленных плавок стали ШХ15.
| N | [C] | [Mn] | [P] | [Cr] | [Ni] | [Cu] | [Si] | [S] |
|---|---|---|---|---|---|---|---|---|
| Плавка N100443 | ||||||||
| 1 | 1.51 | 0.39 | 0.021 | 0.37 | 0.15 | 0.15 | 0.03 | 0.03 |
| 1.53 | 0.34 | 0.024 | 0.49 | 0.16 | 0.10 | 0.18 | 0.044 | |
| 2 | 1.06 | 0.30 | 0.022 | 0.43 | 0.16 | 0.10 | 0.03 | 0.041 |
| 1.04 | 0.20 | 0.021 | 0.37 | 0.19 | н.д. | 0.08 | н.д. | |
| 2 | 0.98 | 0.28 | 0.019 | 0.39 | 0.16 | 0.10 | 0.02 | 0.039 |
| 0.99 | 0.22 | 0.018 | 0.40 | 0.18 | н.д. | 0.03 | н.д. | |
| 3 | 0.97 | 0.24 | 0.019 | 1.27 | 0.18 | 0.10 | 0.15 | 0.037 |
| 0.98 | 0.20 | н.д. | 1.25 | н.д. | н.д. | 0.12 | 0.035 | |
| 5 | 0.99 | 0.28 | 0.020 | 1.53 | 0.18 | 0.10 | 0.36 | 0.012 |
| 1.02 | 0.28 | 0.022 | 1.58 | 0.20 | 0.11 | 0.29 | 0.008 | |
| Плавка N100446 | ||||||||
| 1 | 1.84 | 0.69 | 0.024 | 0.39 | 0.15 | 0.15 | 0.09 | 0.022 |
| 1.83 | 0.52 | 0.019 | 0.39 | 0.27 | 0.09 | 0.13 | 0.036 | |
| 2 | 1.23 | 0.36 | 0.014 | 0.33 | 0.27 | 0.09 | 0.02 | 0.039 |
| 1.24 | 0.25 | 0.012 | 0.36 | 0.27 | н.д. | н.д. | н.д. | |
| 2 | 0.94 | 0.21 | 0.007 | 0.27 | 0.26 | 0.09 | 0.01 | 0.040 |
| 0.94 | 0.21 | 0.014 | 0.30 | 0.24 | н.д. | н.д. | н.д. | |
| 3 | 0.95 | 0.22 | 0.015 | 1.21 | 0.24 | 0.09 | 0.15 | 0.039 |
| 0.96 | 0.22 | н.д. | 1.24 | н.д. | н.д. | 0.19 | 0.030 | |
| 5 | 0.97 | 0.23 | 0.016 | 1.53 | 0.23 | 0.09 | 0.33 | 0.015 |
| 1.01 | 0.22 | 0.016 | 1.53 | 0.23 | 0.09 | 0.30 | 0.016 | |
N пробы: 1 - расплавление, 2 - продувка кислородом, 3 - легирование, 4 - корректировка, 5 - ковшевая проба, н.д. - нет данных. Числитель - расчетные данные, знаменатель - фактические.
Наибольшая ошибка при расчете состава наблюдается в периоде расплавления и окисления, что связано с неизвестным составом завалки, отсутствием расходомеров кислорода при продувке, а также хозяйственной деятельностью предприятия. По остальным пробам согласие хорошее. Максимальная погрешность предсказания состава готового металла по результатам расчетов 30 плавок стали ШХ15 составила по элементам (в процентах): [O] - 0.0005, [Si] - 0.05, [Mn] - 0.06, [P] - 0.005, [S] - 0.005, [Cr] - 0.05. Адаптация проводилась по восьми плавкам, взятым из заводского отчета.
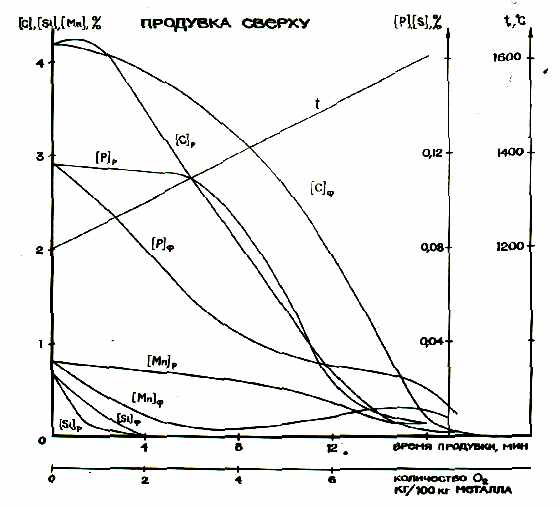
На рис.1 приведена иллюстрация прогнозных возможностей модели по описанию конвертерных процессов. Здесь сравниваются расчетные и фактические составы металла в кислородном конвертере при верхней и нижней продувке. Модель достаточно адекватно описывает донную продувку, которая ближе к равновесию и лучше усреднена по химическому составу, при верхней продувке явно просматривается аккумуляция ванной кислорода и запаздывание окисления примесей. Расчеты проводились без использования каких-либо данных, относящихся к конкретному агрегату.
 |
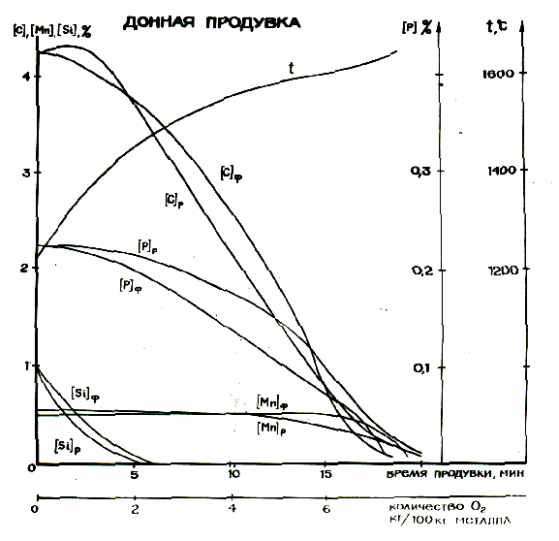 |
Рис. 1. Моделирование кислородно-конвертерного процесса.
© С.А. Храпко, 1990
| Вверх |