Статья посвящена разработке упрощённой модели прогноза температуры металла в дуговой печи. Рассмотрены особенности известных моделей, проанализировано влияние технологических факторов на результаты замеров температуры. Предложен алгоритм, позволяющий учесть влияние "болота" на тепловой баланс плавки и ориентировочно оценить ожидаемую скорость нагрева металла в дуговой печи. Показана существенная роль тепла "болота" и футеровки в процессе расплавления завалки, которое на отдельных плавках достигает 30% от теоретически необходимого тепла.
Дуговая сталеплавильная печь, тепловой баланс, коэффициент нагрева, теплоёмкость, футеровка, тепловые потери.
При выплавке стали в современной дуговой печи особую актуальность приобретает надежность прогноза температуры жидкого металла. Это связано с тем, что для повышения производительности агрегата и снижения себестоимости металла в современной технологии выплавки стали принято совмещение окислительного периода и плавления шихты, в результате чего продолжительность "доводки" металла (после оседания шихты, отбора пробы и замера температуры до выпуска) стала весьма короткой (10-15 минут). На многих заводах производится не более 2-х замеров температуры и отборов проб металла, а иногда и меньше, при этом металл выпускают по расчетной температуре, а результаты 2-й (контрольной) пробы приходят уже после выпуска металла в ковш.
К сожалению, строгий расчёт теплового баланса весьма громоздок и требует большого количества информации, которая либо отсутствует на реальном производстве (например, объём, температура, состав отходящих газов и др.), либо принципиально недоступна в реальных условиях (химический состав, теплопроводность, теплоёмкость, влажность, замусоренность лома и др.). Кроме того, необходимо учитывать, что температурная неоднородность даже только жидкой ванны (разность между замером на поверхности и средней температурой) может достигать 60ºC и более [1,2]
В данной работе рассмотрено влияние массы "болота" на температуру жидкого металла в ДСП.
Обычно в основе большинства систем прогноза температуры лежит допущение, что изменение температуры металла ΔT прямо пропорционально удельному количеству введенной суммарной энергии ΔЕ с некоторым коэффициентом k (ºC/[кВт*ч/т]), зависящим от текущей температуры металла и, иногда, других факторов.
Зависимость указанного коэффициента от температуры обычно объясняется зависимостью тепловых потерь теплопроводностью и излучением от температуры - чем выше температура металла, тем больше потери, и меньше нагрев металла на единицу энергии.
В работе [3] для численного анализа в качестве исходных данных были использованы показатели работы электросталеплавильного комплекса ООО "Электросталь", при этом было проанализировано изменение температуры между двумя замерами на 1730 плавках (3470 экспериментальных точек). В качестве зависимой переменной использовалось отношение прироста температуры ΔT= T2-T1 к удельному расходу суммарной энергии ΔЕ(электрической и альтернативной), в качестве аргумента √ начальная температура металла на интервале. В результате получили следующее уравнение (рис. 1) :
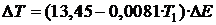 (1)
(1)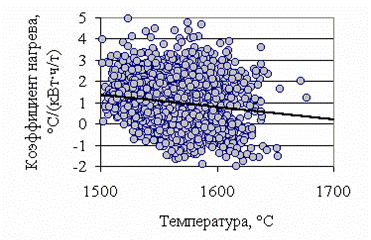
Рисунок 1. Зависимость коэффициента нагрева металла от начальной температуры (T1)
Большой разброс (R=0,50) экспериментальных данных говорит о том, что в типичных условиях современной интенсивной технологии сталеварения по замеренной температуре невозможно однозначно определить (предсказать) ожидаемую скорость дальнейшего нагрева металла, поскольку здесь наблюдается взаимно противоположное влияние двух факторов: с одной стороны, чем выше температура замера, тем будут больше тепловые потери и меньше коэффициент нагрева; с другой стороны, чем выше температура замера, тем более полно расплавлена металлозавалка и можно ожидать более высокий коэффициент нагрева. Возможно, при высокой температуре преобладает влияние первого фактора (поскольку более вероятно полное расплавление металлозавалки), а при низкой - второго, однако определить эту границу не представляется возможным.
Необходима дополнительная информация, характеризующая состояние сталеплавильной ванны. Например, о полноте расплавления завалки можно судить по количеству энергии, введенной в печь к моменту первого замера температуры. Кроме того необходимо учесть, что тепловые потери растут с увеличением времени между замерами, т.е. интервал времени между замерами также должен быть включен в модель. Обработка данных в этом случае дает уравнение (R=0,61) [3]:
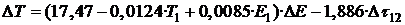 (2)
(2)Знаки и величины полученных коэффициентов не противоречат теоретическим положениям и практике сталеварения. Чем больше температура металла, тем меньше тепловой эффект от вводимой энергии, что объясняется существенным повышением потерь излучением и теплопроводностью. Чем больше величина ввёденной энергии к моменту первого замера, тем меньше осталось в ванне нерасплавленного лома, тем лучше прогрета футеровка, что приводит к повышению коэффициента использования тепла непосредственно на нагрев жидкой ванны. И наконец, время между замерами увеличивает потери тепла - падение температуры металла при простое составляет около 2ºC за минуту, что по порядку величины соответствует реальным данным. К сожалению, среднеквадратическое отклонение (s) для формулы (2) составляет около 30ºC, что явно велико для надежного прогноза температуры. Попытки раздельно учесть электрическую и альтернативную энергию (как в Е1, так и в ΔЕ) не дают существенного повышения коэффициента корреляции R и снижения среднеквадратического отклонения s.
Для повышения точности в формуле (2) желательно также учесть продолжительность плавки (это влияет на величину потерь тепла в период плавления), а также продолжительность межплавочного простоя пустой печи, однако в рассмотренном массиве эти данные отсутствовали.
Имеется ещё одна причина, существенно влияющая на прогноз температуры, которую трудно учесть в простой линейной модели - масса "болота", которая может варьировать в широких пределах, а также масса, теплоёмкость и теплопроводность огнеупорной футеровки.
На рис.2 приведена зависимость первого замера температуры от суммарной введённой энергии к этому моменту. Отношение температуры к введённой энергии изменяется в очень широких пределах - от 3,6 до 5,8ºC/(кВт*ч/т), и в среднем составляет 4,74ºC/(кВт*ч/т). В то же время средняя удельная теплоёмкость железа в интервале температур 0-1600ºC составляет около 0,21 кВт*ч/(т*ºC) (в том числе с учётом теплоты плавления ), что приблизительно соответствует максимально возможному коэффициенту нагрева металла 4,76ºC/(кВт*ч/т). В действительности эта величина должна быть ещё меньше за счет достаточно больших тепловых потерь в ДСП. Средний расход общей энергии за рассмотренный период на данном массиве плавок составляет около 410кВт*ч/т на тонну лома при средней температуре выпуска 1613ºC, что соответствует коэффициенту нагрева 4ºC/(кВт*ч/т) (пунктирная линия на рис.2).
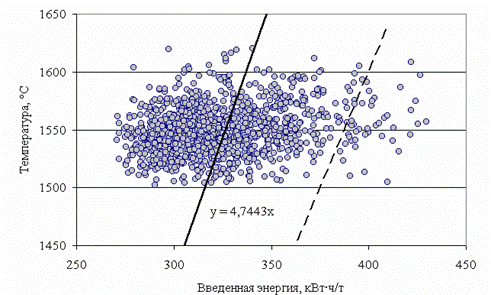
Рисунок 2. Зависимость первого замера температуры (T1) от введенной энергии (E1).
Таким образом, все точки левее пунктирной линии соответствуют дополнительному приходу тепла в ванну до первого замера, а именно, за счет тепла "болота" (и тепла огнеупорной футеровки). Точки справа - скорее всего, плавки после длительных простоев и первые плавки в серии (без "болота").Увеличение массы "болота" хотя и снижает расход тепла на расплавление металлозавалки, однако приводит к тому, что дальнейший нагрев металла до температуры выпуска требует существенно больших затрат тепла (необходимо греть не только завалку, но и "болото"), и это должна учитывать тепловая модель. Хотя достоверные данные о массе "болота" в реальных условиях отсутствуют, её можно ориентировочно оценить по соотношению полученной температуры первого замера и количества введённой энергии.
Упрощённо среднюю температуру металлозавалки к моменту первого замера можно записать в виде:
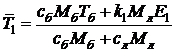 (3)
(3)где cб, Mб, Tб - удельная теплоёмкость, масса и температура болота; cл и Mл - удельная теплоёмкость и масса металлолома; E1 и k1 - суммарная введенная удельная энергия (на тонну металлолома) и коэффициент её использования в период плавления. Числитель представляет собой сумму тепла, вносимого "болотом", и тепла, вносимого энергоносителями (с учётом коэффициента полезного использования). Знаменатель представляет собой суммарную теплоёмкость металлозавалки и "болота".
Реальная температура замера (показания термопары) всегда выше средней температуры:
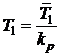 (4)
(4)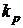 - коэффициент расплавления завалки (
- коэффициент расплавления завалки (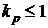 ).
).
Выразив из (3) массу "болота", получим:
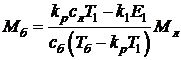 (5)
(5)Температуру последнего замера оценим по следующей формуле (считая, что к концу плавки металлолом полностью расплавлен):
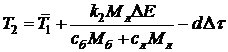 (6)
(6)где ΔE и k2 - введённая удельная энергия (на тонну металлолома) и коэффициент её использования в период нагрева жидкой ванны.
Подставив (5) и (4) в (6), получим выражение для изменения температуры металла между замерами
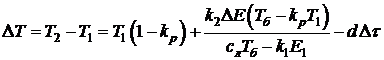 (7)
(7)Отметим, что из (3) (или (4)) в (6) фактически подставляется не масса "болота" 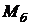 , а произведение
, а произведение 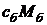 - интегральная теплоёмкость
"болота", в которое в данном случае входит не только фактический остаток
металла от предыдущей плавки, но и часть огнеупорной футеровки, аккумулирующей
тепло в период рафинирования, и отдающей его металлозавалке в период
расплавления. По этой причине попытки рассчитать реальную массу "болота" по
формуле (5) из экспериментальных данных дают завышенные результаты
(20-30 тонн при средней массе выпуска 57-59 тонн), хотя для нашего расчёта это
не принципиально.
- интегральная теплоёмкость
"болота", в которое в данном случае входит не только фактический остаток
металла от предыдущей плавки, но и часть огнеупорной футеровки, аккумулирующей
тепло в период рафинирования, и отдающей его металлозавалке в период
расплавления. По этой причине попытки рассчитать реальную массу "болота" по
формуле (5) из экспериментальных данных дают завышенные результаты
(20-30 тонн при средней массе выпуска 57-59 тонн), хотя для нашего расчёта это
не принципиально.
В первом приближении примем, что коэффициент расплавления завалки линейно зависит от температуры замера по интерполяционной формуле:
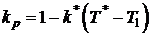 (8)
(8)Подстановка (8) в (7) дает конечную расчётную формулу:
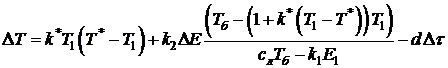 (9)
(9)Обработка имеющихся данных с использованием пакета Statistica даёт следующие значения параметров формулы (9), при этом стандартная ошибка полученной формулы составляет менее 20ºC (R=0,71, всего 1178 плавок):
k1 = 0,897; k2 = 0,170; k*= 0,0004;
T* = 1605ºC; Tб = 1610,5ºC; d = -1,54ºC/мин;
cл = 0,252 кВт*ч/(т*ºC).
Интересно, но средняя температура "болота" Tб оказалась очень близка к средней по данному массиву температуре выпуска металла из печи, которая составляет 1613ºC. Эффективность использования тепла в период расплавления k1(до первого замера температуры) составила 90%, а в период нагрева k2 - в 5 раз меньше, что также совпадает с наблюдаемыми на практике величинами. Следует отметить, что в упрощённой модели не учитывалось влияние отдаваемых шлакообразующих (около 35 кг/т лома) и моментов их отдачи (например, в бадью или в ванну непосредственно перед замером). Возможно именно шлакообразующие а также влага и замусоренность металлолома (6-8%, т.е. 60-80 кг/т лома) и привели к несколько завышенной оценке теплоёмкости металлозавалки по сравнению с теплоёмкостью чистого железа (теплоёмкость извести и других оксидов составляет около 0,33кВт*ч/(т*ºC), а известняка и доломита - ещё выше, что в сумме ориентировочно и дает полученную величину cл. Кроме того, для анализа был использован практически "сырой" массив исходных данных, т.е. не производились ни фильтрация недостоверных замеров, ни отсев плавок после длительных простоев и т.д. Тем не менее, полученные коэффициенты по порядку величины не противоречат интуитивно ожидаемым - температура "болота" и температура полного расплавления ванны, коэффициенты использования тепла в периоды расплавления и нагрева жидкой ванны, потери тепла ванной при простоях соответствуют общепринятой практике сталеварения.
Таким образом, предложенный алгоритм позволяет ориентировочно оценить ожидаемую скорость нагрева металла в ДСП и с приемлемой точностью прогнозировать текущую температуру сталеплавильной ванны. Проведенный анализ свидетельствует о существенной роли тепла "болота" и тепла, аккумулированного футеровкой в процессе расплавления завалки - на отдельных плавках до 30% от теоретически необходимого.
Список литературы:
1. Об оценке температурной неоднородности ванны сталеплавильного агрегата. Скрябин В.Г., Скрябин Д.В., Кучеренко О.Л., Старосоцкий А.В., Храпко С.А. Теория и практика металлургии, 2004.- №6. -С.18-21.
2. Модель расчёта средней температуры металла в сверхмощной ДСП и ее применение в АСУТП. В.Г. Скрябин, Д.В. Скрябин. Материалы 2-й международной научно-практической конференции "Автоматизированные печные агрегаты и энергосберегающие технологии в металлургии" (3-5 декабря 2002 г.,Москва).- М.: МИСиС. - С. 466-468.
3. Прогноз температуры металла в дуговой печи. Храпко С.А., Серов А.И. Сборник трудов ДонНТУ, вып. №11 (159) А, Донецк, 2009г. - С. 66-72.