Металлургия и обработка металлов (выпуск 5)
Материалы научно-технической конференции молодых ученых физико-металлургического факультета
Донецк: ДонНТУ. 2002. С. 43—45.

Динамическая математическая модель аргонной продувки стали в ковше

А.А. Филипишин, В.Г. Скрябин

Донецкий национальный технический университет
г. Донецк, Украина

Продувке стали аргоном посвящено много работ, в которых предложены уравнения и математические модели позволяющие рассчитать только изменение концентрации водорода. Но, интерес представляет изменение концентрации и других газообразующих элементов в металле (кислород, углерод, азот, сера), состава и расхода отходящих газов.

Рассчитать эти величины можно на детерминированной динамической математической модели. Вывод основных уравнений изменения состава металла и отходящих газов сделан на основе достижения термодинамического равновесия в системе газовый пузырёк-металл и баланса масс:

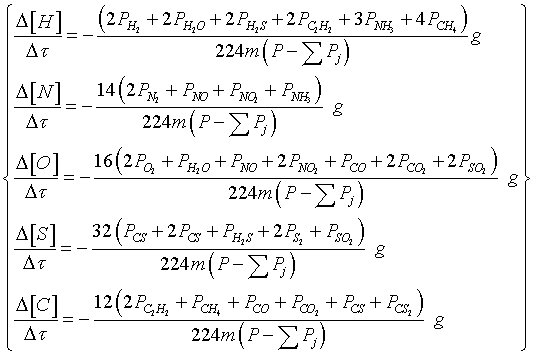
где m – масса стали, т; [Н], [N], [О], [S], [С] – концентрация элемента в стали, %; Р – внешнее давление, атм; 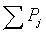 – сумма парциальных давлений всех газов, кроме Р_Ar, атм;  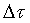– шаг времени продувки, мин; g – расход аргона, м³/мин.

Приняты допущения: аргон чистый, в данный момент времени температура и состав стали одинаковые в любой точке объёма, шлаковая фаза на процесс дегазации не влияет, поглощение газов из внешней среды не происходит, газы в пузырьке идеальные, давление в пузырьке равно внешнему (гидростатическое давление металла не учитывалось).

Чтобы уменьшить число неизвестных до пяти, уравнения преобразованы с привлечением зависимостей для констант равновесия реакций дегазации и образования j-газов. Преобразованная система уравнений стала основой для разработки математической модели продувки, информационная схема которой представлена на рисунке 1.

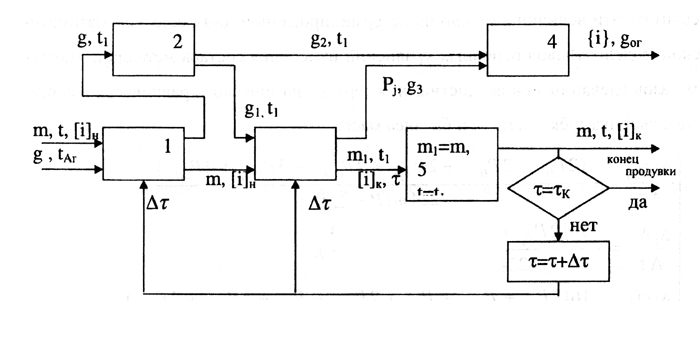
1 – теплообменник; 2 – делитель; 3 – реактор; 4 – смеситель; 5,6 – блоки переприсваивания и условия

Рисунок 1 – Информационная схема процесса.

Входами модели являются масса, температура и химический состав стали (m, t, [i]_н); расход и температура аргона (g, 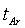); шаг и конечное время продувки (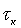, 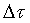). В теплообменнике (1) рассчитывается температура металла при охлаждении аргоном. В делителе (2) поток аргона (g) условно разделяется на два (g₁ и g₂). С потоком g₁ коэффициент достижения термодинамического равновесия пузырек аргона – металл равен 1, а с потоком g₂ – равен нулю. В реакторе (3) решается система дифференциальных уравнений численным методом 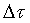Рунге-Кутта, рассчитываются за шаг времени состав стали ([i]_к), уменьшенная масса стали (m₁), парциальные давления всех газов (P_j) и их расход (g₃3). В смесителе (4) рассчитывается состав {i} и расход (g_ог) отходящего газа. В блоке (5) входным величинам присваиваются конечные значения, полученные на предыдущем шаге.

Модель настраивали изменением величины коэффициента в делителе (2), сравнивая расчётные результаты с лабораторными экспериментами [Изв. вуз. Черная металлургия. – 1961, №2. – с. 22-30]. Начальные время продувки, температуру, расход аргона и состав стали задавали такой же: t=1600 С, g=0.5 м³/мин, [Н]=0.0012%, [С]=0.9%, [S]=0.004%. He приведенные содержания азота и кислорода приняли: [N]=0.016%, [0]=0,001%.

Результаты сравнения представлены в таблице 1. Наилучшая адекватность модели получена при значении коэффициента достижения равновесия 0.295.

Таблица 1 – Изменение состава стали при продувке

Из табл. 1 следует, что при продувке аргоном уменьшается концентрация растворенных [Н] и [N], а содержание [S], [О], [С] практически не изменяется. Расход отходящих газов (g_ог) уменьшается по ходу продувки и составил: на 1 мин – 1.705, а на 5 мин – 0.699 м³/мин. Коэффициент использования аргона процесса дегазации для данных экспериментальной продувки оценен равным 0.295.

© А.А. Филипишин, В.Г. Скрябин, 2002