Труды 4-го конгресса сталеплавильщиков. Москва, 1997, C. 35—40.

Управление сталеплавильными процессами на основе современных физико-химических представлений

А.Г. Пономаренко, П.И. Окоукони, С.А. Храпко, Е.Н. Иноземцева

Интенсивные исследования в области термодинамики и физической химии металлургических систем в середине XX в. создали теоретическую базу для превращения металлургии из области, основанной преимущественно на опыте и интуиции, в науку, опирающуюся на строгий математический фундамент. В настоящее время на огромном числе конкретных примеров показано, что практически весь комплекс физико-химических процессов металлургической технологии поддается расчету с точностью, достаточной для построения высокоэффективных информационно-вычислительных систем управления плавкой и проектирования технологии. В сочетании с возможностями современных средств вычислительной техники это делает реальным резкое сокращение традиционного разрыва между теорией и производственной практикой, превращение теории в удобный и надежный инженерный инструмент управления и выработки новых технологических решений.

Вместе с тем, существующие компьютерные системы управления сталеплавильными агрегатами, даже наиболее совершенные из числа реализованных к настоящему времени, практически полностью ориентированы только на исполнение режимов, задаваемых технологами. Физико-химические параметры процесса остаются вне сферы, управления и оптимизации. Работа таких систем основывается на статистических моделях, синтезируемых путем обработки массивов данных прошлых плавок, или на простом копировании режимов и операций одной из предыдущих плавок, принятой за норму. Очевидно, что для успешной работы подобных систем требуется выполнение весьма жестких условий в отношении качества и стабильности поставок сырья, энергоносителей, работы вспомогательных служб, что достигается только при существовании разветвленной инфраструктуры обеспечивающих производств. Это делает понятной причину низкой эффективности подобных систем управления плавкой, внедренных на ряде отечественных предприятий, сталеплавильные агрегаты которых вынуждены систематически работать в «запредельных» режимах.

Детерминированная физико-химическая модель плавки, в отличие от статистической, исходит из строгого априорного расчета, опирающегося на базы фундаментальных законов и констант, поэтому ее прогностические возможности неизмеримо шире. Система управления плавкой, построенная на основе детерминированной физико-химической модели, должна в масштабе реального времени генерировать технологические решения, поддерживая работу агрегата в любых «нештатных» ситуациях, совместимых с принципиальной возможностью выполнения задания (например, получение жидкого металла требуемого состава и температуры). Адекватность управляющих действий такой системы обеспечивается за счет обратной связи (адаптация, самообучение). Кроме того, появляется возможность «проигрывать» мыслимые варианты плавки при проектировании новой технологии — функция, принципиально недоступная для статистических моделей.

В докладе обсуждаются проблемы, возникающие при построении детерминированных моделей плавки, и приводятся практические результаты работы по созданию реальной системы управления, основанной на этом принципе.

Одна из главных проблем информатизации состоит в своего рода «инвентаризации» практически необъятного объема накопленных знаний, относящихся к предмету, его структурировании и содержательном анализе в рамках определенным образом организованной системы терминов и понятий, т.е. в системе определенного языка. В области точного естествознания, частными приложениями которого являются технические науки, таким систематизирующим языком служит язык классической механики Ньютона с его жесткой математической структурой. Теоретическая металлургия, первоначально формировавшаяся как раздел высокотемпературной химии, сохранила в основном описательный, трудноалгоритмизируемый язык этой науки. Для систематизации теоретического материала, относящегося к металлургическим расчетам, принципиально важными оказались работы Гиббса, интерпретирующие термодинамику как обобщение классической механики на тепловые явления. Именно это позволяет представить практически весь комплекс методов количественного описания явления сталеплавильного процесса, включая и кинетические, в виде компактной системы взаимосогласованных алгоритмов и программ.

Так, термодинамический анализ химического процесса обычно начинается с его представления в виде некоторого уравнения реакции, отражающей материальный баланс при образовании (или распаде) тех или иных химических соединений. Принятое уравнение реакции определяет вид записываемого на следующем шаге выражения закона действующих масс, всех последующих преобразований и конечного результата. Однако до настоящего времени не найдено прямых экспериментальных методов или общих правил определения вида химических соединений, которые следует принять при написании исходной реакции в конденсированных системах, например, при описании распределения серы (или любого другого элемента) между металлом и шлаком. Один и тот же процесс может быть представлен практически неограниченным множеством комбинаций различных реакций, что приводит к неоднозначности результатов термодинамического анализа в целом. Таким образом, уже на первом шаге мы встречаемся с принципиально неформализуемой процедурой.

Не меньшие трудности возникают при математической формализации правил и законов химической кинетики и термодинамики необратимых процессов, исходным пунктом которых в большинстве случаев остается все та же химическая реакция.

Метод Гиббса позволяет описывать химические процессы в любых системах без предварительного их представления в виде стехиометрических реакций. Более того, феноменологическая (классическая, формальная, макроскопическая) термодинамика Гиббса дает как раз тот язык, с помощью которого можно наиболее просто объяснить сущность любой задачи исключительно в терминах непосредственно измеряемых величин, таких как температура, давление, химический состав, объем, масса и др., т.е. величин, которыми руководствуется технолог в своей работе. По своей математической структуре термодинамика Гиббса — это классическая механика (статика сплошных сред) с той разницей, что механика изучает системы, способные обмениваться только работой и веществом, а термодинамические системы обмениваются еще и теплом. Для этого в исходные уравнения механики Гиббс вводит дополнительную переменную, характеризующую способность системы отдавать или поглощать тепло — энтропию. Таким образом, термодинамика приобретает совершенно строгую математическую структуру механики. Термодинамику Гиббса можно рассматривать как обобщение механики на реальные системы, движение которых всегда сопровождается тепловыми явлениями.

При этом оказывается, что многие эмпирические законы и правила химии (в частности закон действующих масс) закономерно следуют из первичных постулатов термодинамики в виде различных частных случаев, но уже в форме строгих математических зависимостей. Становится очевидной некорректность широко распространенного мнения о том, что классическая термодинамика описывает лишь равновесия, а расчет скоростей и других характеристик процессов нуждается в особой системе представлений и понятий.

Механика исходит из положения, что состояние (полная совокупность свойств) системы взаимосвязанных тел при отсутствии внешних полей полностью определено в любой момент ее движения (существования), если известен вид связи между телами, образующими систему, и заданы значения двух параметров, характеризующих общее количество вещества системы и ее способность обмениваться работой — в простейшем случае масса (m) и объем (V) — в один из моментов.Математически этот постулат выражается уравнением:

(1)

При переходе к более общему случаю термодинамических систем вводится энтропия (S), как некоторый параметр, характеризующий способность системы отдавать или получать тепло

(2)

Это выражение лежит в основе технической термодинамики, имеющей дело с веществом постоянного состава. Термодинамика Гиббса становится химической в результате замены общей массы (m) массами k компонентов, образующих систему

(3)

Энтропия, объем и масса, входящие в эти выражения, представляют минимально необходимый набор первичных понятий, не интерпретируемых на уровне феноменологической (макроскопической) теории. Все другие свойства, рассматриваемые в термодинамике, являются их производными (как в обычном, так и математическом смысле этого слова), образуя специфический язык термодинамики с его жесткой логической структурой. Так, внутренняя энергия системы (как и любое другое ее свойство) является некоторой функцией этих переменных

(4)

Дифференциал внутренней энергии как функции нескольких переменных имеет вид

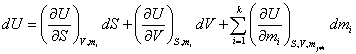
(5)

Производные этого выражения могут рассматриваться как определения температуры, давления и химических потенциалов компонентов

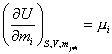
(6)

Точно так же определяется теплоемкость, модуль упругости и другие понятия, составляющие язык термодинамики. С учетом (6) обозначений выражение (5) принимает вид

(7)

Это выражение представляет одну из общих форм фундаментального уравнения, которое при известном виде функции (4) позволяет выполнять практические расчеты. Преобразованием уравнения (7) можно получить другую его форму

(8)

Выражения (7) и (8) можно представить в виде

	(9)
	(10)

где		–	время;
		–	пространственная координата.

Эти выражения связывают обобщенные потоки и силы, что позволяет систематизировать задачи кинетики и термодинамики необратимых процессов в терминах единого макроскопического языка.

Чтобы перейти к решению практических задач, нужно определить конкретный вид функций (4) для фаз, участвующих в процессе. Для этого необходимо использовать знания о свойствах частиц, образующих вещество, химической связи, о формах существования компонентов в металле и шлаке, диффузионной подвижности частиц и т.д. и т.п., что приводит к практически неограниченному объему информации, представляющему плохо организованное множество фактов, их толкований, гипотез, специфических понятий и др. Вновь возникает проблема систематизирующего языка, поскольку понятия классической термодинамики (температура, давление, энтропия и др.) в применении к явлениям микромира лишены смысла, а также проблема интерпретации результатов микроскопического рассмотрения свойств вещества на языке феноменологической термодинамики. Эту функцию выполняет специально созданный раздел механики, названный статистической механикой.

Следует отметить особенности этого метода, учтенные при получении конкретного вида функции (4) для металлургических расплавов. Существенные отличия от известных зависимостей при этом получены для шлаковой фазы. Особенности этих функций сводятся к следующему:

1. компонентами всех конденсированных фаз считаются элементы Периодической системы;

2. при подсчете статистической суммы единицами теплового движения считаются атомы (остовы) химических элементов, образующих фазу, и электроны;

3. число компонентов равно числу элементов, образующих фазу, электроны не являются независимыми компонентами, фаза в целом остается электронейтральной.

Введение электронов в качестве самостоятельной единицы теплового движения позволило исключить необходимость написания уравнений реакций в конденсированных фазах и единообразно описать электрохимические, поверхностные явления, а также явления, изучаемые в теории полупроводников. При этом выражение для химического потенциала компонента конденсированной фазы имеет следующий вид

(11)

где		–	атомная доля элемента;
		–	коэффициент активности элемента i без учета электронного вклада;
		–	валентность элемента i;
		–	химический потенциал электронов в шлаке (уровень Ферми), который удобно выразить, например, через активность (парциальное давление) любого элемента системы, в частности кислорода:

(12)

В случае металлов член в выражении (11) — электронный вклад — мало изменяется с составом, поэтому при расчетах равновесия с вполне достаточной точностью можно использовать обычное выражение

(13)

при этом

Теперь равновесный коэффициент распределения примесного элемента между металлом и шлаком может быть получен из простого равенства химических потенциалов этого элемента в обеих фазах:

(14)

Подставив значения для химических потенциалов из (11)–(13) в выражение (14), получаем для коэффициента распределения элемента i между металлом и шлаком:

(15)

Аналогично рассмотрев распределение серы между шлаком и газовой фазой, приходим к широко известному уравнению сорбционной способности шлака по отношению к сере:

(16)

Резко упрощается описание равновесий в случае фаз сложного состава, включая и производственные расплавы. Так, для расчета количества и состава продуктов, получающихся при проплавлении завалки известного состава, записываются уравнения материальных балансов распределения элементов по образующимся фазам (для простоты предположим, что образуются только две фазы — металл и. шлак):

(17)

где		–	масса элемента i поступившая с шихтой (задана);
		–	массы элемента i, перешедшие в металл и шлак соответственно (требуется определить).

Всего имеется k (число компонентов) таких уравнений, в которых содержится 2k неизвестных. Записываем далее k условий равновесия (14). Таким образом, получаем 2k уравнений и 2k неизвестных, кроме того, необходимо задать температуру и давление системы, поскольку они входят в выражения для химических потенциалов. Полученные массы компонентов металла и шлака дают полную информацию о составе и количестве этих фаз. Разбив плавку на периоды между добавками и повторяя расчет, можно проследить за изменениями состава металла и шлака на протяжении всей плавки в равновесном приближении. Учет кинетических сдвигов реального процесса входит в функции системы адаптации к конкретным условиям и учитывает то обстоятельство, что отклонения от равновесия носят систематический характер (смещение в сторону исходного состояния). На этой основе был создан пакет прикладных программ «Оракул», позволяющий имитировать плавку в научных и учебных целях. На практике мастеру приходится решать обратную задачу — по заданному составу конечного металла рассчитывать состав завалки и текущих добавок. Поэтому был разработан вариант решения обратной задачи, в которой задаются материалы, имеющиеся на складе, и марка выплавляемой стали. Система рассчитывает оптимальный по стоимости состав завалки и всех текущих добавок, включая шлакообразующие.

Расчет оптимальных количеств шлакообразующих материалов, обеспечивающих требуемый уровень дефосфорации, десульфурации, а также эффективное усвоение легирующих и раскислителей, является уникальной способностью системы ОРАКУЛ. В отличие от известных систем расчета легирующих добавок, основанных на линейных моделях равномерного смещения, система ОРАКУЛ использует не среднестатистические коэффициенты усвоения, которые в действительности зависят от индивидуальных условий каждой плавки, а вычисляет их путем совместного решения задачи оптимизации шихты и термодинамического расчета распределения элементов в системе металл–шлак. Это существенно повышает точность расчета и эффективность оптимального управления процессом. Задача решается путем вычисления матрицы дифференциальных коэффициентов усвоения , определяемых из текущего распределения элементов в ванне и отражающих изменение массы элемента i в металле при добавлении элемента j в систему. В упрощенном виде (без учета газовой фазы) распределение элементов между металлом и шлаком определяется из следующей системы уравнений

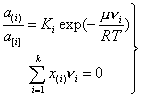
(18)

Выражая все величины через массы элементов, получим, что в общем виде задана система уравнений

(19)

которая решается относительно при заданных , откуда по правилу неявного дифференцирования получим в матричных обозначениях

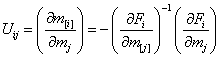
(20)

Состав металла с использованием указанных коэффициентов усвоения в матричном виде вычисляется с помощью системы из 2k неравенств

(21)

где	Fн, Fв	–	векторы нижнего и верхнего пределов состава металла;
	M	–	вектор исходных масс элементов в металле;
	B	–	матрица состава материалов;
	I	–	единичный вектор;
		–	вектор изменения (приращения) масс материалов.

Приведение (21) к линейному виду и переход к неравенствам по составу металла дает систему, которую можно решить симплекс-методом.
К системе (21) могут быть также добавлены любые другие возможные технологические или организационные ограничения, в частности, требования к минимальной и максимальной массе получаемого металла, к общей массе (или объему) вводимых шихтовых материалов, к массе или доле (относительно общей массы шихты) отдельных материалов (или групп материалов, объединенных по определенному признаку), к составу, количеству и свойствам шлака, а также ограничения наличия материалов на складе и т.д.

Решение сформированной таким образом системы неравенств дает новый набор шихтовых материалов , обладающий минимальной стоимостью, после чего расчет повторяется при . Итерации прекращаются, а расчет считается законченным при выполнении условия

(22)

где

–

заранее заданная малая величина, определяющая требуемую точность результатов расчета.

Интересно, что в процессе решения расчетные массы рекомендуемых шихтовых материалов претерпевают значительные изменения — взаимное исключение или замена одних материалов другими, из чего можно сделать вывод, что система может самостоятельно находить решения, приводящие к экстремуму целевой функции (минимальные затраты).

В основе реализованной вычислительной процедуры лежит двойственный линейный симплекс-метод решения задачи линейного программирования в комбинации с оригинальным компактным алгоритмом «отложенных» вычислений, что придает ей исключительное быстродействие и практически полностью снимает ограничения по количеству оптимизируемых элементов и шихтовых материалов (например, система нормально функционирует в масштабе реального времени при 50 элементах и 400 видов используемых материалов на ЭВМ класса IBM AT286/287).

Кроме того, при практической реализации алгоритма существенное повышение надежности расчета достигается путем детального учета факторов неопределенности химических составов используемых шихтовых материалов, массы и состава исходного металла, используемых констант распределения элементов между металлом и шлаком и т.д.

Возможны случаи, представляющие особый интерес для практики, когда решение указывает на невозможность гарантированного попадания в требуемый состав в той или иной ситуации (отсутствие необходимых ферросплавов, ошибка во взвешивании и т.п.). В таких случаях система заблаговременно, в начале периода плавки, выдает соответствующее сообщение и, благодаря способности анализировать причины возможного отклонения, предлагает перечень оперативных решений: снизить неопределенность заданных параметров (уточнить состав того или иного ферросплава, массу задаваемых материалов и т.д.); легировать в два приема с промежуточной пробой металла; перевести плавку в другую марку в соответствии с имеющимся портфелем заказов или в любую стандартную марку. По всем возможным вариантам сообщается новая шихтовка, сумма затрат и ожидаемый состав металла. В автоматическом режиме возможно самостоятельное принятие решения системой в пределах заранее заданного перечня и приоритетов. Вся информация о фактически полученном составе металла используется в системе адаптации параметров модели, учитывающих неравновесность реального процесса в зависимости от медленных изменений параметров агрегата с учетом периода плавки, марки стали и др.

Система ориентирована на работу в автоматическом режиме с выдачей сигнала непосредственно на исполнительные механизмы, а также на работу в режиме советчика сталевара с выдачей рекомендаций и комментариев к фактическим действиям персонала. Вместе с тем она является достаточно гибкой для использования при ретроспективных анализах, краткосрочном и перспективном планировании в технологических разработках, оценки эффективности новых технологических решений и др. Система может быть использована при управлении самыми различными процессами производства стали, однако при разработке в первую очередь имелось в виду управление плавкой в ДСП и внепечной обработкой.

Обсуждены некоторые проблемы построения информационно-технологических систем управления сталеплавильными процессами на базе детерминированной физико-химической модели плавки и возможности таких систем. Приводится описание системы управления технологией плавки ОРАКУЛ, синтезированной на этой основе. Пакет «Оракул» разрабатывался для управления полностью автоматизированными агрегатами выплавки и внепечной обработки стали, однако может широко использоваться в режиме советчика сталевара при ручном управлении, гарантируя попадание в состав при минимальных затратах практически на любых марках стали.

© А.Г. Пономаренко, П.И. Окоукони, С.А. Храпко, Е.Н. Иноземцева, 1997