Известия ВУЗов. Черная металлургия. 2003. №11. С. 8—10.

О корректном использовании метода Лагранжа при выводе критериев равновесия Гиббса

С.А. Храпко

Донецкий национальный технический университет, Украина

В литературе критерии равновесия (со ссылкой на Гиббса) выводятся следующим образом: утверждается, что равновесному состоянию закрытой многофазной системы соответствуют экстремальные значения термодинамических потенциалов системы (минимум энергии Гиббса G, максимум энтропии S и т.д.) при условии постоянства соответствующих термодинамических переменных (для S—E и V, для G—p и T) и выполнении уравнений материального баланса. Для практического использования этот критерий обычно записывают в виде производных, т.е. в терминах химических потенциалов.

Считается, что такая постановка задачи является обычным поиском условного экстремума функции многих переменных при наличии уравнений связи между независимыми переменными (ограничений) в виде равенств, что приводит к использованию метода Лагранжа. Общий ход дальнейших рассуждений заключается в следующем.

1. Выбирается определенный термодинамический потенциал многофазной системы (равный сумме соответствующих потенциалов отдельных фаз), например, свободная энергия:

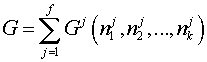(1)

где 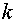 — число компонентов системы; 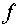 — число возможных фаз; 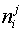 — количество компонента 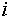в фазе .

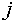2. Записываются условия постоянства соответствующих выбранному потенциалу термодинамических переменных (в данном случае — p и T) и ограничения материального баланса на суммарные количества каждого компонента системы. Последние в простейшем случае (все фазы состоят из одинаковых компонентов) имеют вид

,

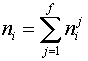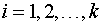(2)

где 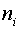 — общее количество компонента  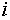в системе.

3. Записывается функция Лагранжа в виде суммы рассматриваемой функции и всех имеющихся ограничений, помноженных на «неопределенные множители Лагранжа»:

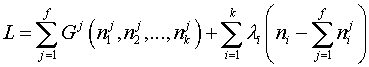(3)

где 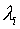 — неопределенные множители Лагранжа.

4. Производится поиск безусловного экстремума полученной функции (производные по всем независимым переменным, в том числе по неопределенным множителям, должны быть равны нулю). Число получаемых при этом уравнений строго равно числу неизвестных, т.е. система должна иметь единственное решение. В результате получают критерии равновесия в виде равенства во всех фазах температуры, давления и химических потенциалов компонентов, образующих замкнутую систему:

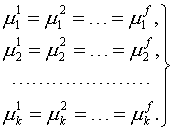(4)

Уравнения (4) совместно с (2) дают систему из 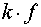 уравнений и неизвестных и определяют равновесный состав системы.

Указанный ход рассуждений действительно принадлежит Гиббсу, однако практическое использование такого критерия равновесия для расчета состава многофазной многокомпонентной системы требует некоторых дополнений.

Условие равенства химических потенциалов и давления во всех интересующих нас фазах (т.е. во всех возможных в данной системе) является достаточным, но не необходимым условием.

Более точно указанные критерии равновесия необходимо сформулировать в следующем виде: если установилось состояние равновесия, то во всех образовавшихся фазах (и только в них) температура, давление и химические потенциалы будут равны. Обратное утверждение, вообще говоря, неверно — записав систему уравнений с равенством химических потенциалов во всех возможных в данных условиях фазах мы можем и не получить равновесный состав системы (решения просто не будет — система окажется несовместной).

Для устранения этой проблемы в литературе фигурируют туманные рассуждения, что каких-то фаз (или отдельных компонентов в определенных фазах) может не быть в состоянии равновесия, если в этих фазах, существование которых возможно в данных условиях, даже при бесконечно малом количестве компонента его химический потенциал будет больше, чем в остальных фазах. В этом случае предлагается исключить такие условия равновесия и добавить вместо них условия равенства нулю масс соответствующих компонентов (попросту говоря, исключить эти фазы или компоненты из рассмотрения).

В общем виде проблему можно сформулировать следующим образом. Чтобы найти равновесный состав системы (перечень фаз и количества каждого компонента в них), нужно записать (и затем решить) соответствующую систему уравнений. Однако для этого необходимо знать фазовый состав системы, который станет известным лишь после нахождения ее равновесного состава и который не известен заранее.

Указанная проблема вовсе не порочит метод Гиббса или использованный метод Лагранжа. Дело в том, что Гиббс, рассматривая термодинамику как формальную схему, допускал отрицательные массы фаз. В этом случае система уравнений для любого набора фаз всегда будет иметь соответствующее решение (даже если в ответе будут фигурировать отрицательные массы).

В практических расчетах реальных равновесий отрицательные массы фаз не имеют физического смысла. Формальный анализ приведенной выше схемы рассуждений указывает на то, что при составлении функции Лагранжа пропущены условия неотрицательности масс компонентов в фазах (подразумевается, что это и так ясно):

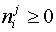(5)

На самом деле, это такие же дополнительные условия (ограничения), как и условия материального баланса, только в виде неравенств, а не уравнений. Учет в функции Лагранжа (либо в виде дополнительных ограничений, либо в результате замены переменных) после выполнения описанных выше преобразований приводит к следующей формулировке критериев химического равновесия:

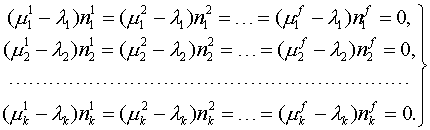(6)

В отличие от (4), в систему уравнений (6) могут быть записаны абсолютно все фазы, существование которых возможно в данной системе, даже если их количество будет превышать количество независимых компонентов (т.е. противоречить правилу фаз). В результате решения «лишние» фазы будут исключены из ответа (их массы станут равными нулю). При этом уравнения (6) останутся справедливыми и в ситуации отсутствия каких-либо компонентов или фаз: при строго нулевой массе компонента или фазы соответствующие уравнения становятся тождеством и автоматически исключаются из системы уравнений.

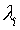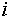Неопределенные множители Лагранжа  в (6) имеют простой физический смысл — химический потенциал компонента  в системе. Решение каждого уравнения в (6) естественным образом распадается на два случая. Если в состоянии равновесия компонент 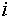 присутствует в фазе 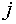, то его химический потенциал в этой фазе должен быть равен химическим потенциалам этого же компонента во всех остальных фазах, имеющихся в состоянии равновесия. Если же компонента 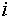нет в фазе 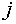, то на его химический потенциал никаких ограничений не накладывается (уравнение становится тождеством).

Таким образом, система уравнений (6) совместно с (2) и (5) имеет 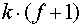неизвестных и уравнений и позволяет корректно поставить и решить задачу определения количества и состава фаз в равновесном состоянии. Система является более общим критерием равновесия, чем (4), поскольку учитывает случаи произвольного (не известного заранее) набора фаз в состоянии равновесия.

Недостаточность (4) проявляется и в других приложениях метода Гиббса.

Например, предлагается (Пономаренко А.Г. Вопросы термодинамики фаз переменного состава, имеющих коллективную электронную систему // ЖФХ. — 1974. — Т.48. — №7. — С. 1668—1674; № 8. — С. 1950—1958) считать компонентами оксидных и солевых фаз химические элементы Периодической системы Менделеева, при этом для такой фазы добавляется условие электронейтральности

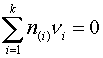(7)

а на основе привлечения дополнительных предположений относительно физической природы шлака в уравнение химического потенциала компонента солевого раствора вводится дополнительное слагаемое

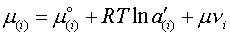(8)

где 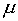 — химический потенциал электронов или уровень Ферми (не контролируемый никакими методами анализа), 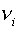 — степень окисления элемента 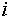в фазе.

В действительности необходимость введения в (8) дополнительного слагаемого 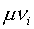и дополнительных предположений относительно физической природы шлака отсутствует. Дл этого достаточно учесть, что (7) является таким же дополнительным условием (ограничением), как и (2), поэтому его необходимо включать в функцию Лагранжа (3) наравне со всеми остальными ограничениями. В простейшем случае (система металл—шлак) получим:

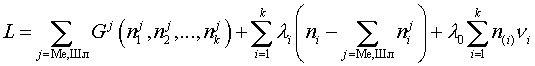(9)

Дифференцируя (9) по неизвестным и приравнивая полученные производные нулю, получим (в случае постоянных ):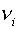

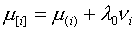(10)

Величина 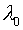вычисляется одновременно с составами фаз при решении системы уравнений (2), (7), (10) и имеет определенный физический смысл, характеризуя, например, окисленность системы (её можно связать с уровнем Ферми 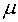, парциальным давлением кислорода 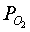и т.д.).

Таким образом, формулы (8)—(10) являются обычным следствием метода Гиббса и получаются «автоматически» при корректной постановке задачи расчета равновесного состава многофазной системы.

Уравнение (10) при подстановке 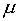в качестве 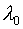можно интерпретировать следующим образом: 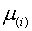представляет собой «внутренний» (т.е. «ионный») химический потенциал элемента 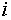в фазе, а  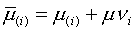— изменение энергии Гиббса фазы при добавлении электронейтрального атома 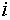(вместе с 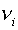электронами), т.е. «внешний» («видимый» другими фазами) химический потенциал элемента .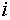

Интересно отметить, что использование величин 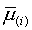для вычисления свободной энергии шлака в виде

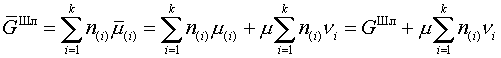(11)

дает для электронейтральной фазы исходное выражение для свободной энергии шлака (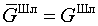), поскольку второе слагаемое в в соответствии с тождественно равно нулю.

Однако использование (11) в (3) сразу приводит к результату (10) без привлечения (7) в качестве дополнительного ограничения. Более того, уравнение (7) получается автоматически при дифференцировании функции Лагранжа (3) по переменной :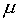

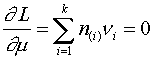(11)

т.е. выражение (11) уже содержит «внутри себя» ограничение на состав шлака (7).

Выводы. Таким образом, проведенный анализ свидетельствует о том, что при выводе критериев равновесия методом неопределенных множителей Лагранжа для получения корректных результатов в число дополнительных условий необходимо включать все известные априорные данные как в виде уравнений, так и в виде неравенств (такие, как ограничения материального баланса, неотрицательности масс компонентов фаз, электронейтральности оксидных фаз и другие).

© С.А. Храпко, 2003