| Публикации: | АСУТП | Теория и технология | Научные работы | Главная |
Известия ВУЗов. Черная металлургия. 2004. №9. С.
Одна из самых важных и сложных задач в сталеварении– расчет химического состава и температуры металла. Именно адекватный прогноз позволяет эффективно решать задачи непосредственного управления технологическими процессами выплавки и обработки стали, а также весь круг сопутствующих задач, предназначенных для повышения эффективности работы металлургического агрегата, цеха и предприятия в целом.
Система прогнозирования строится на основе физико-химических закономерностей протекания сталеплавильных процессов. Термодинамика и кинетика взаимодействия металла и шлака в сталеплавильных агрегатах изучались многими исследователями [1]. Значительное количество работ посвящено анализу перехода химических элементов через межфазную границу и собственно, кинетике элементарного акта химической реакции. В настоящее время большинство исследователей пришли к выводу, что процессы взаимодействия в пограничном слое и на межфазной границе не являются лимитирующей стадией окисления примесей в промышленных агрегатах [2]. Считается, что основное «торможение» перехода системы из начального состояния в равновесное (при отсутствии внешних воздействий) связано с доставкой компонентов из циркуляционного объема на границу раздела «металл-шлак». Тем не менее, математическое описание обычно построено на классических уравнениях молекулярной диффузии [1,3]. Движущей силой потока компонента из одной фазы в другую принимается разность текущей и равновесной концентраций (или активностей). В качестве коэффициента пропорциональности используется «эффективный» коэффициент диффузии или коэффициент «турбулентной» диффузии, превышающий коэффициент молекулярной диффузии на 6-8 порядков. Получаемые в результате одно- и двумерные системы дифференциальных уравнений, во-первых, имеют высокую вычислительную сложность при попытках реализовать эти модели для описания реальных процессов. Во-вторых, применимость таких моделей для неспокойной жидкой ванны в реальных агрегатах очень сомнительна, поскольку с физической точки зрения весьма неправдоподобна «индивидуальность» коэффициентов диффузии и движущих сил по каждому элементу при мощных конвективных потоках, когда все элементы «едут вместе в одном трамвае».
Перспективным подходом при описании кинетики процессов взаимодействия фаз является использование равновесного термодинамического расчета в качестве основы. Стоит учесть, что стремление системы к равновесию– пожалуй, единственный известный строго доказанный факт. Для реализации этого подхода необходимо:
Для численного решения предпочтительно использовать критерии равновесия в виде[4]:
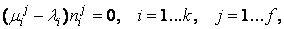 |
(1) |
где 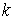 – число компонентов системы
(элементов Периодической системы Менделеева);
– число компонентов системы
(элементов Периодической системы Менделеева); 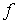 – максимальное число
рассматриваемых фаз;
– максимальное число
рассматриваемых фаз; 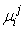 ,
, 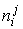 –
химический потенциал и количество элемента
–
химический потенциал и количество элемента
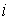 в фазе
в фазе 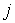 ;
; 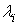 – неопределенные множители Лагранжа.
– неопределенные множители Лагранжа.
Уравнение состояния 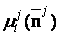 определяет индивидуальность
любой фазы. Многолетний опыт решения практических задач позволил сделать
следующий выбор. Термодинамическое состояние элемента в шлаке описывается с
помощью теории регулярных ионных растворов В.А. Кожеурова [5] и теории субрегулярных ионных
растворов Г.Г. Михайлова [6] с учетом дополнительного вклада энергии мезофазных переходов. Для расчета коэффициентов
активности компонентов металла выбрана теория субрегулярных растворов[7]. В настоящее время это единственные
надежные и широко доступные методы расчета активностей, обеспеченные численными
значениями параметров.
определяет индивидуальность
любой фазы. Многолетний опыт решения практических задач позволил сделать
следующий выбор. Термодинамическое состояние элемента в шлаке описывается с
помощью теории регулярных ионных растворов В.А. Кожеурова [5] и теории субрегулярных ионных
растворов Г.Г. Михайлова [6] с учетом дополнительного вклада энергии мезофазных переходов. Для расчета коэффициентов
активности компонентов металла выбрана теория субрегулярных растворов[7]. В настоящее время это единственные
надежные и широко доступные методы расчета активностей, обеспеченные численными
значениями параметров.
К сожалению, пришлось отказаться от метода коллективизированных электронов (МКЭ) [8] из-за низкой точности расчета активностей, и от метода параметров взаимодействия Вагнера[9], которые дают принципиально неверный ход кривой активности в области повышенных концентраций, не согласуются с уравнением Гиббса-Дюгема и законом Рауля, особо опасны для экстраполяции [7].
Для расчета равновесного состояния можно использовать один из известных алгоритмов, например, приведенный в работе [10].
Расчет траектории перехода системы из исходного состояния в конечное проводился с использованием следующих основных положений:
В этом случае расчет производится следующим образом [4]. Из общего объема металла и шлака условно выделяется «реакционная зона» (РЗ) и «циркуляционный объём» (ЦО). Принимается, что поверхностные слои металла и шлака (находящиеся в «реакционной зоне») приходят в равновесие. За счет конвективных потоков в объемах фаз через некоторое время эти поверхностные слои заменяются новыми порциями металла и шлака, между которыми снова устанавливается равновесие. Выводимые поверхностные слои поступают в циркуляционные объемы металла и шлака, где усредняются, после чего весь расчет повторяется.
Для численного моделирования задается шаг по времени 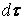 , массы
металла и шлака в РЗ (
, массы
металла и шлака в РЗ (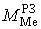 ,
,
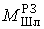 ) и скорость смены
РЗ (
) и скорость смены
РЗ (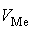 ,
,
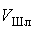 ).
Без особой погрешности можно принять, что РЗ полностью обновляется за
рассматриваемый период времени
).
Без особой погрешности можно принять, что РЗ полностью обновляется за
рассматриваемый период времени 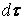 , т.е.
, т.е. 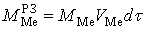 и
и 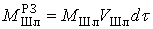 , где
, где
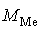 и
и
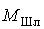 – общая
масса металла и шлака.
– общая
масса металла и шлака.
В качестве примера вычисления траектории перехода системы
в равновесное состояние рассмотрим закрытую систему металл-шлак (без газовой
фазы, без продувки кислородом, кипения металла, поступления материалов, при
постоянной температуре). Введем следующие обозначения: 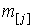 ,
, 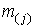 – текущая масса элемента
– текущая масса элемента 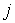 в металле и шлаке;
в металле и шлаке; 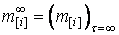 ,
, 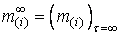 –
конечные (равновесные) массы элементов в металле и шлаке;
–
конечные (равновесные) массы элементов в металле и шлаке; 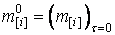 ,
, 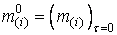 – начальные массы элементов в металле и шлаке.
– начальные массы элементов в металле и шлаке.
В этом случае для состава металла по прошествии интервала
времени 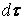 получим
следующее выражение:
получим
следующее выражение:
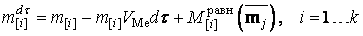 , , |
(2) |
где 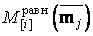 – функция, вычисляющая массу
элемента
– функция, вычисляющая массу
элемента 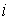 в
металле, если система, состоящая из
в
металле, если система, состоящая из 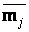 масс элементов, придет в
равновесие;
масс элементов, придет в
равновесие; 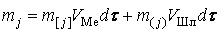 – текущая суммарная масса элемента
– текущая суммарная масса элемента
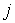 в РЗ.
в РЗ.
Первое слагаемое в (2) соответствует текущей массе элемента в металле, второе – массе элемента, переходящей из ЦО в РЗ и третье –
массе элемента, «возвращающейся» из РЗ в ЦО после перехода РЗ в равновесное
состояние. Анализ показывает, что (2) имеет непосредственное аналитическое
решение, только если скорости перемешивания металла и шлака (т.е. скорости
смены РЗ) одинаковы (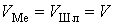 ). В этом случае, учитывая условия
задачи и однородность первого порядка функций
). В этом случае, учитывая условия
задачи и однородность первого порядка функций 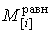 , получим:
, получим:
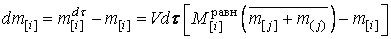 . . |
(3) |
Поскольку 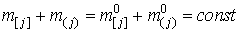 – исходный суммарный состав
системы (неизменный в процессе перехода в равновесное состояние, поскольку
считаем систему закрытой), то
– исходный суммарный состав
системы (неизменный в процессе перехода в равновесное состояние, поскольку
считаем систему закрытой), то 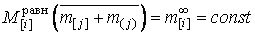 – конечный (равновесный) состав
металла, откуда
– конечный (равновесный) состав
металла, откуда
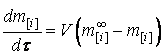 . . |
(4) |
Если скорость перемешивания металла и шлака постоянна во
времени (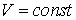 ),
то можно разделить переменные и проинтегрировать:
),
то можно разделить переменные и проинтегрировать:
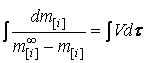 , , |
(5) |
откуда
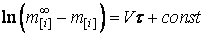 . . |
(6) |
В результате получаем экспоненциальную зависимость состава металла от времени:
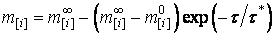 , , |
(7) |
где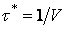 –
постоянная времени (по нашим оценкам в современных промышленных дуговых
сталеплавильных печах порядок величины
–
постоянная времени (по нашим оценкам в современных промышленных дуговых
сталеплавильных печах порядок величины 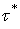 ориентировочно составляет
1÷10 минут, в зависимости от условий и периода плавки).
ориентировочно составляет
1÷10 минут, в зависимости от условий и периода плавки).
Для иллюстрации проведен расчет по рассмотренной модели при следующих условиях: в ковш с металлом (после раскисления и легирования) сливается окисленный печной шлак с достаточно высоким содержанием оксида марганца. Начальный состав металла – 0.4% C, 0.3% Si, 0.9% Mn, 0.05% S, 0.027% P, масса – 100 тонн; начальный состав шлака – 25% SiO2, 23% FeO, 8% Al2O3, 28% CaO, 7% MgO, 8% MnO, 0.4% P2O5, 0.6% CaS, масса – 12 тонн; температура металла – 1600 °С. Расчет равновесного состава дает следующие результаты: металл – 0.4% C, 0.003% Si, 0.47% Mn, 0.065% S, 0.036% P; содержание FeO в шлаке – 4.6%.
Численное интегрирование выражения дает идентичные уравнению зависимости (см. рис. 1). Аналогичным образом изменяется и состав шлака.
Формула (7) хорошо согласуется с общепринятым описанием процессов в теории автоматического
регулирования, кроме того, похожий результат получается при классическом
диффузионном рассмотрении указанного процесса перехода системы в равновесное
состояние как диффузионного переноса компонентов под действием градиента
концентраций (активностей) [1,3]. Строго говоря, используемые в
кинетике коэффициенты «турбулентной диффузии» являются попыткой учесть реальный
макроскопический массоперенос классическими диффузионными уравнениями, однако
отличная от диффузии природа рассматриваемых явлений приводит в некоторых
случаях к совершенно иным зависимостям. Например, расчет дает экспоненциальное
поведение состава металла и шлака только при одинаковых скоростях перемешивания
этих фаз (рис. 1). В то же время, в условиях типичного сталеплавильного
производства металл и шлак, как правило, имеют разную температуру, вязкость, и
следовательно, разную скорость перемешивания, что существенно изменяет
результаты расчета кинетики взаимодействия фаз. Например, в сталеразливочном
ковше (во время отстоя) температура, вязкость и скорость перемешивания шлака
ниже, чем аналогичные параметры металла. На рис. 2 приведены результаты расчета
для таких условий (при 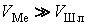 ).
).
Интересно, что в начальный период времени (первые 7 минут в приведенном примере) содержание марганца в металле увеличивается, несмотря на то, что равновесное содержание марганца в металле ниже исходного содержания, т.е. изменяется в сторону, противоположную конечному равновесному состоянию! В то же время в диффузионных уравнениях невозможен переход через равновесное состояние (как и изменение концентрации в противоположную от равновесия сторону), т.к. у химических элементов нет «инерции» – при достижении равновесной концентрации происходит исчезновение движущей силы. Кроме того, при индивидуальной диффузии каждого компонента не может быть взаимного влияния компонентов и их потоков друг на друга.
Несмотря на кажущееся противоречие, такое «антиравновесное» поведение марганца легко объясняется высоким («сверхравновесным») содержанием кремния в металле в этом же интервале времени: пока содержание кремния не снизилось до равновесных значений, идет восстановление марганца и фосфора из шлака кремнием, растворенным в металле. После «выгорания» кремния направление процесса перехода марганца и фосфора изменяется на обратное– происходит их снижение до равновесных значений. Возможно, этот эффект может объяснить появление взаимодействия потоков в термодинамике необратимых процессов.
Для иллюстрации этого положения был проведен расчет траектории перехода системы в равновесное состояние при импульсном воздействии, т.е. в рассмотренном количественном примере системы металл-шлак, пришедшей в равновесие, из шлака в металл мгновенно перенесена некоторая часть кремния (а массы всех остальных элементов оставлены неизменными). Полученные металл и шлак приняты в качестве начального химического состояния системы. Результаты расчета траектории перехода системы в равновесное состояние при различных скоростях перемешивания представлены на рис. 3 (одинаковые скорости перемешивания фаз) и рис. 4-5 (отличающиеся скорости перемешивания). Несмотря на то, что исходный состав металла практически совпадает с конечным по всем элементам (за исключением кремния), из рисунков видно, что под действием «потока» кремния при отличающихся скоростях перемешивания взаимодействующих фаз происходит возникновение «потоков» всех остальных элементов.
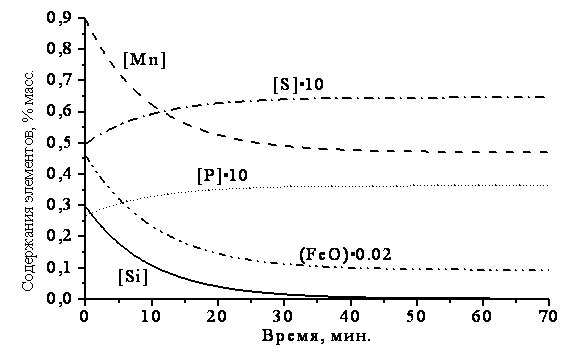
Рисунок 1 – Расчет состава металла и
шлака при легировании на сливе (одинаковые скорости перемешивания, мин-1)
мин-1)

Рисунок 2 – Расчет состава металла и шлака при легировании на сливе
(отличающиеся скорости перемешивания,  мин-1)
мин-1)

Рисунок 3 – Расчет состава металла и шлака при импульсном воздействии
(одинаковые скорости перемешивания,  мин-1)
мин-1)
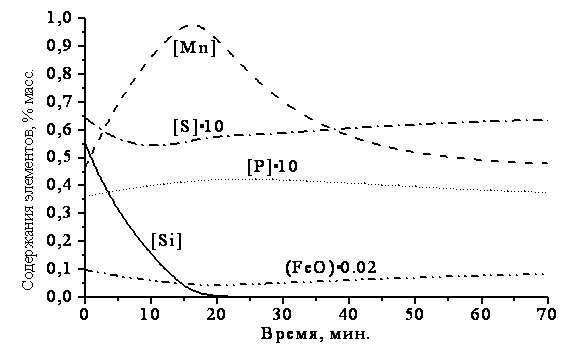
Рисунок 4 – Расчет состава
металла и шлака при импульсном воздействии (отличающиеся скорости перемешивания,
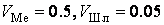 мин-1)
мин-1)
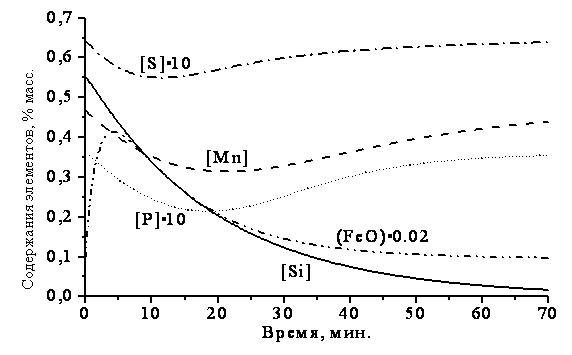
Рисунок 5 – Расчет состава металла и шлака при импульсном воздействии
(отличающиеся скорости перемешивания, 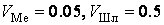 мин-1)
мин-1)
При этом в начальной части всех графиков содержание всех
элементов изменяется в сторону, противоположную равновесному состоянию.
Возможно, подобная модель позволяет вычислить феноменологические коэффициенты
Онзагера. Интересно, что «антиравновесное» изменение состава металла и шлака наблюдается
при любых неравных скоростях перемешивания фаз: 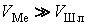 (рис.4), или
(рис.4), или 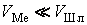 (рис. 5).
Единственным условием является неравенство скоростей перемешивания фаз – чем
больше их отличие, тем больше отличается от «экспоненциального» поведение примесей.
(рис. 5).
Единственным условием является неравенство скоростей перемешивания фаз – чем
больше их отличие, тем больше отличается от «экспоненциального» поведение примесей.
Как показали многочисленные расчеты, неидеальность фаз не является определяющим фактором, поскольку изменение способа расчета активности компонентов только незначительно сдвигает равновесное состояние, не изменяя общего хода кривых. Аналогичная ситуация и с величинами констант равновесия – их изменение влияет только на равновесный состав и не изменяет принципиально вид зависимостей. Кроме того, результаты численного анализа показывают, что наибольшее влияние на поведение системы оказывает меньшая величина из скоростей перемешивания фаз, а увеличение большей скорости сверх определенного предела практически не влияет на ход кривых.
Практическая ценность учета подобного поведения примесей может быть весьма существенной. Например, если в момент максимального содержания марганца в металле произвести отлив шлака из ковша, то можно существенно повысить усвоение марганца из ферросплавов.
Аналогичным образом может быть учтен массоперенос при вычислении распределения температуры по глубине ванны. Аналитическое решение при постоянных скоростях перемешивания и нагрева металла дает для перегрева поверхности ванны над температурой металла на подине зависимости вида:
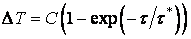 . . |
(8) |
где 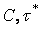 – параметры, определяемые из
геометрии ванны и интенсивности перемешивания.
– параметры, определяемые из
геометрии ванны и интенсивности перемешивания.
Например, расчетом получено, что в условиях дуговой
сталеплавильной печи ДСП-100 перегрев может достигать 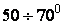 и более (в
зависимости от условий), что подтверждается экспериментами.
и более (в
зависимости от условий), что подтверждается экспериментами.
Важный элемент предлагаемой модели – учет гидродинамики сталеплавильной ванны, а именно, расчет интенсивности перемешивания (т.е. скоростей потоков металла и шлака). С нашей точки зрения этот расчет должен основываться на уравнении изменения кинетической энергии металла [4]:
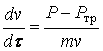 . . |
(9) |
где 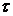 –
время, с;
–
время, с; 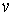 – скорость потоков металла,
м/c;
– скорость потоков металла,
м/c; 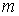 – масса металла,
кг;
– масса металла,
кг; 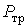 ,
,
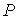 –
мощность сил трения и перемешивающих сил (пузыри оксидов углерода; струя вдуваемого кислорода, инертный газ, вдуваемый через
донные фурмы и т.д.), Вт.
–
мощность сил трения и перемешивающих сил (пузыри оксидов углерода; струя вдуваемого кислорода, инертный газ, вдуваемый через
донные фурмы и т.д.), Вт.
Такой расчет позволил численно предсказать наблюдаемые особенности протекания процесса пульсирующего окисления углерода при кипении сталеплавильной ванны [4].
Рассмотренный подход позволяет провести декомпозицию протекающих в ванне процессов и описать изменение химического состава металла и шлака практически в любом металлургическом агрегате (ДСП, конвертер, сталеразливочный ковш, установка «печь-ковш», вакууматор, промежуточный ковш и т.д.).
На основе разработанной модели построена компьютерная система моделирования «АСУТП– ОРАКУЛ» для автоматического проектирования и управления технологическими процессами выплавки и внепечной обработки стали [11]. Система реализована на Молдавском (г. Рыбница) и Белорусском (г. Жлобин) металлургических заводах, прошла промышленное опробование, внедрена и дала существенный экономический эффект, выражающийся в стабилизации режима, снижении продолжительности плавки, расхода электроэнергии и металлолома на тонну годного.
Таким образом, проведенные расчеты траектории перехода системы в равновесное состояние показывают принципиальную возможность временного изменения содержания элементов в сторону, противоположную конечному равновесному состоянию под действием потока другого элемента, что можно назвать взаимодействием потоков. Предложенная модель позволяет адекватно описать изменение химического состава металла и шлака в металлургических агрегатах и построить эффективные автоматизированные системы управления технологическими процессами.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
| Вверх |