| Публикации: | АСУТП | Теория и технология | Научные работы | Главная |
Изв. ВУЗов, Черная металлургия, 1991, №12, С. 49—52.
Термодинамика исходит из предположения (иногда его называют нулевым законом), что все свойства вещества в состоянии равновесия взаимосвязаны и могут быть выражены с помощью некоторой функции — уравнения состояния (в терминологии Гиббса — фундаментального уравнения), например,
| | (1) |
где | P, V и T | – | давление, объем и температура; |
| mi | – | массы компонентов системы; | |
| n | – | число компонентов системы. |
Если известен точный вид уравнений состояния для каждой из фаз системы, то точное вычисление равновесных свойств каждой из фаз и системы в целом сводится к чисто формальным преобразованиям. Но термодинамика постулирует лишь сам факт существования уравнений состояния, точный их вид ни для одной из реально существующих фаз не известен. Во всех приложениях термодинамики к реальным объектам мы вынуждены использовать те или иные приближенные зависимости - модели фаз, разработка которых является предметом термодинамической теории растворов.
К настоящему времени предложено весьма большое число таких моделей (теорий), в основном в виде зависимости термодинамических свойств от состава:
| | (2) |
где | M=(m1,m2...mn) | – | вектор состава фазы. |
Проблеме построения моделей посвящены многочисленные исследования, существует множество подходов к ее решению, однако модели остаются средоточием главных трудностей в практических приложениях термодинамики. Необходимость систематизации, обобщения и единообразного представления накопленного материала с целью создания баз и банков данных внесла новые аспекты в указанную проблему. В настоящем исследовании с этой точки зрения рассматриваются некоторые вопросы, связанные с представлением уравнений состояния степенными рядами.
Для расчета активностей компонентов металлических систем в настоящее время широко используется метод параметров взаимодействия К. Вагнера [1], обеспеченный численными значениями параметров для большинства используемых в металлургии элементов. Основу метода составляет разложение соответствующей парциальной избыточной термодинамической функции смешения (энергии Гиббса ΔGie, энтальпии ΔHi, энтропии ΔSie) в степенной ряд Тейлора (Маклорена) по концентрациям компонентов и обратной температуре около точки, отвечающей чистому растворителю. Если за стандартное состояние принять чистый компонент i, то для избыточной свободной энергии, точнее для lnγi=ΔGie/RT при постоянных температуре и давлении получим:
| | (3) |
где | xi | – | мольная доля компонента i в фазе; |
| r | – | индекс, обозначающий растворитель; | |
| γi и γio | – | коэффициенты активности компонента i в произвольной точке и в точке xr=1 соответственно. |
Здесь и далее суммирование производится от единицы до n, а частные производные соответствуют точке чистого растворителя (xr=1). Входящие в уравнение частные производные называют параметрами взаимодействия и обозначают соответственно εij, ρij и ρij,k. С учетом этих обозначений выражение (3) принимает вид:
| | (4) |
Аналогичные выражения можно записать для ΔHi и ΔSie. Наиболее часто используют формулы Вагнера в виде ряда, в котором отброшены слагаемые выше первого порядка.
В точке xr=1 параметры имеют строгий термодинамический смысл, а следовательно, единственное значение, к которому должны стремиться накапливаемые экспериментальные величины. Это и является основой для табулирования таких данных. Разложение Вагнера (как и любой ряд) можно использовать и в концентрационном интервале (фактически оно так и используется), однако параметры разложения при этом утрачивают свойства термодинамически обоснованных констант, становятся обычными коэффициентами аппроксимирующего полинома, характеризуют частный массив данных и должны приводиться с указанием интервала составов, в котором производилось определение численных величин параметров. Однако в литературе часто не различают параметры Вагнера, как фундаментальные константы вещества и частные аппроксимирующие коэффициенты. Поэтому не случайно, что приводимые различными авторами значения "параметров Вагнера" могут не совпадать по знаку и порядку величины, не соблюдается требуемое теорией тождество εij = εji. Табулирование таких данных утрачивает упомянутую выше строгую основу, на которой, собственно, базируется метод Вагнера.
Не имеют теоретического обоснования и противоречат смыслу разложения функции в ряд, введение концентрационной зависимости параметров взаимодействия первого порядка в случаях, когда полином первой степени не дает желаемых результатов [2,3], равно как и попытки раздельного определения и сопоставления параметров взаимодействия первого порядка в различных концентрационных интервалах или различных сплавах (например, для разбавленных и насыщенных растворов [4, 5]). Неудачным следует признать использование разложения Вагнера для аппроксимации свойств растворов во всем диапазоне составов [6], даже при одновременном повышении степени полинома (что само по себе приводит к резкому увеличению необходимого числа параметров, их взаимной корреляции и утрате основных достоинств метода), из-за невыполнения уравнения Гиббса-Дюгема, предельного закона Рауля, невозможности преобразований с целью определения других свойств, проверки на термодинамическую устойчивость и др. Особенно опасна экстраполяция в сторону концентрированных растворов за пределы первичного массива данных (см. рисунок). В этой части кривая обычно резко отклоняется от опытной и не выходит на требуемую выбором стандарта точку чистого вещества (γi=1 при xi=1).
К существенному улучшению представления парциальных функций приводит учет дополнительного условия в виде уравнения Гиббса-Дюгема, выражающийся в добавлении слагаемого γr. На этом основан "квадратичный формализм" Даркена [7] для бинарных растворов и формулы "модифицированного формализма параметров взаимодействия" Пелтона [8] для фаз произвольного состава:
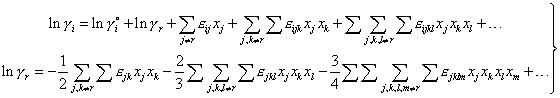 | (5) |
где | εij, εijk, εijkl,... | – | параметры модели, причем εij = εij = εji |
Формулы (5) позволяют при том же числе эмпирических параметров повысить точность аппроксимации (см. рисунок 1), используя существующие численные значения параметров и вид формул Вагнера, причем в области разбавленных растворов они сводятся к разложению Вагнера, а при использовании параметров взаимодействия первого порядка эквивалентны "квадратичному формализму" Даркена, расширенному на многокомпонентные растворы.
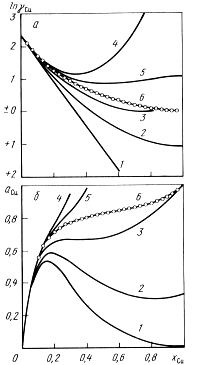 |
Рисунок 1. Экстраполяция зависимостей ln γCu (а) и aCu (б) от состава системы Fe - Cu с использованием параметров Вагнера, вычисленных из эксперимента [14] в точке xCu=0: 1, 4 и 2, 5 - по формулам Вагнера (4) и Пелтона (5); 3, 6 - ТСР (10); точки - данные [14]; 1...3 - учет параметров первого порядка; 4...6 - учет параметров первого и второго порядков. |
Вместе с тем формулы (5) по-прежнему не содержат требование γi=1 в точке xi=1 и непригодны даже для грубых экстраполяционных оценок в области концентрированных растворов. Естественным развитием этого метода представляется введение еще одного дополнительного термодинамического условия, связанного с предельным законом Рауля. Известно, что отношение коэффициентов активности вещества i в чистом веществе i и при его бесконечном разбавлении в растворителе j равно γi o(j). В случае выбора в качестве стандартных состояний чистых жидких компонентов это эквивалентно учету точки чистого вещества, в которой его активность и коэффициент активности равны единице, т. е.
| | (6) |
Этим достигается повышение точности аппроксимации и прогностических возможностей формул (экстраполяция заменяется более безопасной интерполяцией). Например, на основании уравнений (5), (6) можно написать
| | (7) |
Таким образом, в формулах (5) дополнительно учитывается тождество, задающее взаимосвязь между собственными параметрами. Учет точек чистых компонентов позволяет отказаться от определения параметров взаимодействия второго и третьего порядков по экспериментальным данным и рассчитывать их исходя из известных значений γio и εij. При этом для формул (5) первого порядка получим
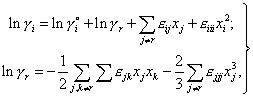 | (8) |
где | 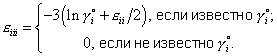 |
Присутствие в этих формулах параметров более высокого порядка не означает необходимость в дополнительных экспериментальных данных - они на основании соотношения (7) могут быть вычислены, например, из известных параметров Вагнера более низкого порядка. Нетрудно убедиться, что для уравнений (8) выполняется уравнение Гиббса-Дюгема, а также предельные законы Рауля и Генри при любых значениях εij, γio и xi, что позволяет обоснованно их использовать для описания других термодинамических свойств фазы во всем диапазоне составов. Аналогичные соотношения могут быть получены для полиномов произвольного порядка и произвольного выбора стандартного состояния компонентов.
Однако общим решением проблемы является переход к разложениям интегральных функций вместо парциальных. Анализ показывает, что формулы (4), (5) первого порядка по точности аппроксимации и числу эмпирических параметров эквивалентны теории регулярных растворов (ТРР), а выражения (8) - теории субрегулярных растворов (ТСР) с субрегулярным поведением в системах i - r и регулярным в системах i - j, а полная ТСР эквивалентна уравнениям (8) второго порядка с нулевыми параметрами трехчастичного взаимодействия (εijk = 0 при i ≠ j ≠ k).
ТРР и ТСР являются разложением в степенной ряд интегральных функций (с сохранением параметров первого и второго порядка соответственно), в них "автоматически" учитываются все упомянутые выше термодинамические требования. Выражение для избыточной мольной энергии Гиббса и коэффициентов активности в этом случае имеет вид [9]:
| | (9) |
| | (10) |
где | Wij | – | параметры модели (так называемые теплоты смешения). |
В литературе [10] отмечается, что ТСР позволяет описывать большинство металлических систем с достаточной для практических расчетов точностью. При необходимости ТСР так же, как и разложение Вагнера, позволяет повысить точность аппроксимации за счет дополнительного учета параметров более высокого порядка, как это предлагается в работе [11].
Одной из причин недостаточно широкого использования ТСР является отсутствие численных значений параметров. Для их определения можно использовать имеющиеся данные по параметрам взаимодействия Вагнера первого и второго порядков и значения γio в различных растворителях. Продифференцировав уравнение (10) по мольной доле соответствующего компонента (с учетом dxr / dxi = -1 ), для бинарной (l - r) и тройной (l - m - r) систем получим
| | (11) |
| | (12) |
| | (13) |
Для систем l - r возможно раздельное определение параметров Wrl и Wlr по уравнениям (11), (12), т.е.
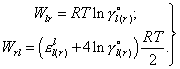 | (14) |
Если компонент l в чистом виде - газ или неизвестно значение γio(r) (т.е. для раздельного определения параметров Wrl и Wlr недостаточно данных), то, приняв регулярное поведение компонентов в системе l - r, из выражения (12) получим
| | (15) |
Для систем l - m известен только один параметр εlm(r) = εml(r), поэтому, также приняв регулярное поведение компонентов в системе l - m, из выражения (13) найдем
| | (16) |
Полученные формулы позволяют описывать металлические растворы во всем диапазоне составов, причем в области малых концентраций примесей уравнение (10) будет давать результаты, совпадающие с расчетами по формуле Вагнера, а при повышенных концентрациях его можно более обоснованно использовать для оценок в отсутствие экспериментальных данных (рис. 1).
Помимо параметров взаимодействия Вагнера, может быть использован опытный материал, накопленный в виде теплот смешения, параметры Вагнера в растворах на основе других растворителей, константы распределения примесей в системе металл - газ и другие. При этом имеется возможность дополнительно систематизировать экспериментальную информацию.
Выводы. Использование теории субрегулярных растворов с расчетом параметров модели по параметрам взаимодействия Вагнера [12] в термодинамической модели распределения элементов между металлом, шлаком, газовой фазой [13] позволяет получить более высокую корреляцию расчетных и экспериментальных данных во всей области составов.
© С.А. Храпко, А.Г. Пономаренко, 1991
| Вверх |