Рассмотрены различные варианты формул теории субрегулярных растворов для многокомпонентных систем. Рассчитаны значения коэффициентов для рассмотренных формул. Показано, что корректный выбор вида формул позволяет более обоснованно использовать их в трех- и многокомпонентных системах, особенно по которым нет (или имеется ограниченное количество) экспериментальных данных.
1. Общие положения
Для вычисления термодинамических функций высокотемпературных металлургических расплавов (в частности, при расчете диаграмм состояния) широкое распространение получили различные варианты теории регулярных (ТРР) и субрегулярных растворов (ТСР). При расчете энергии смешения в многокомпонентном растворе формулы ТСР, в том числе и теории субрегулярных ионных растворов (ТСРИР, отличие состоит только в способе вычисления концентраций компонентов) обычно записывают в виде:
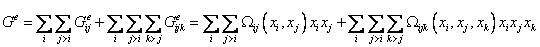 , (1)
, (1)где
![]() – вклад двойной системы
– вклад двойной системы ![]() в суммарную энергию смешения;
в суммарную энергию смешения;
![]() – вклад тройной системы
– вклад тройной системы ![]() в энергию смешения,
в энергию смешения, ![]() – концентрация компонента
– концентрация компонента ![]() .
.
Первое слагаемое – сумма двойных взаимодействий по всем бинарным системам, которые
имеются в рассматриваемой многокомпонентной системе, второе слагаемое – то же
самое, но для тройных систем. При необходимости, аналогичным образом можно
учесть взаимодействия и в системах более высокого порядка (четверные системы и
выше). Функции ![]() и
и ![]() –
по сути, это теплоты смешения, как в ТРР, но с концентрационной зависимостью.
–
по сути, это теплоты смешения, как в ТРР, но с концентрационной зависимостью.
Рассмотрим вклады бинарных систем. В литературе предлагаются различные варианты формул для вычисления вклада каждой бинарной системы в суммарную энергию смешения (для упрощения индексы коэффициентов бинарных систем опущены). Например, рассмотрим 3-х параметрические формулы:
Г.Г. Михайлов (ТСРИР) [1]:
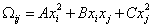 , (2)
, (2)К. Люпис ([3], с. 252-255):
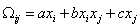 , (3)
, (3)трехпараметрический аналог формулы Келлога [4]:
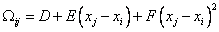 , (4)
, (4)Т.Г. Сабирзянов [5]:
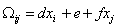 , (5)
, (5)Предлагаемый в данной работе вариант формулы ТСР:
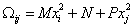 . (6)
. (6)2. Пересчет параметров бинарных систем из одной модели в другую
Рассмотрим чистую двойную систему 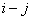 , в которой
, в которой 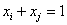 . В этом случае нетрудно показать (подставив
. В этом случае нетрудно показать (подставив ![]() ), что формулы (2)-(4) и (6) полностью идентичны
друг другу по виду зависимости от состава системы и представляют собой
квадратичную параболу (с тремя коэффициентами). Если известны коэффициенты для
одной их формул, то параметры остальных легко вычисляются, например, если
известны A, B и C, то:
), что формулы (2)-(4) и (6) полностью идентичны
друг другу по виду зависимости от состава системы и представляют собой
квадратичную параболу (с тремя коэффициентами). Если известны коэффициенты для
одной их формул, то параметры остальных легко вычисляются, например, если
известны A, B и C, то:
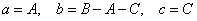 , (7)
, (7)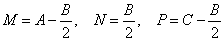 , (8)
, (8)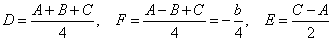 . (9)
. (9)Результаты пересчета при известных параметрах [1, 2], принятых за базовые
[1],
приведены в табл. 1. Единственным исключением является формула (5): в двойной системе
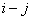 за счет
за счет
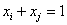 она приводит, например, к виду:
она приводит, например, к виду:
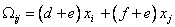 , (10)
, (10)т.е. к уравнению прямой линии, у которого всего 2 коэффициента, и вычислить независимо 3 параметра формулы (5) по данным о свойствах граничной бинарной системы невозможно, поэтому в дальнейшем эта формула не рассматривается.
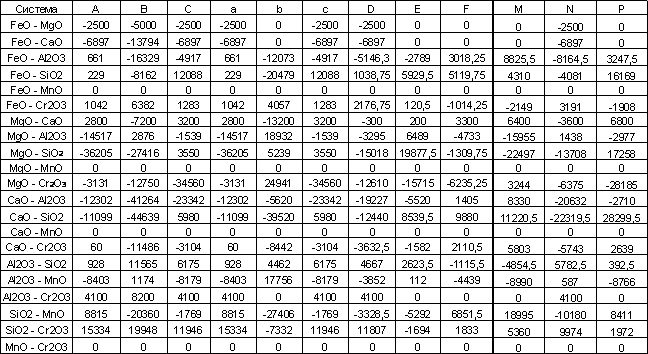 <
<Принципиальное отличие формул проявляется лишь в том случае, если рассматривается не двухкомпонентная, а многокомпонентная система. Например, если какая-то бинарная система подчиняется регулярному поведению, то это соответствует таким значениям параметров и виду формул:
Формула Г.Г.Михайлова (2):
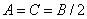 ,
,
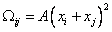 ,
,
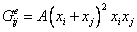 . (11)
. (11)Формула Люписа (3):
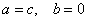 ,
,
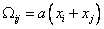 ,
,
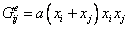 . (12)
. (12)Формула Келлога (4):
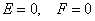 ,
,
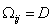 ,
,
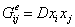 . (13)
. (13)Формула (6):
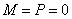 ,
,
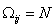 ,
,
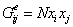 . (14)
. (14)Все приведенные формулы абсолютно идентичны, если 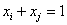 , однако дают принципиально отличающиеся зависимости в многокомпонентной системе
(когда
, однако дают принципиально отличающиеся зависимости в многокомпонентной системе
(когда 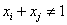 ). Отличие формул очевидно: при
разбавлении системы
). Отличие формул очевидно: при
разбавлении системы 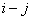 в многокомпонентной
системе ее вклад в суммарную теплоту смешения зависит от вида используемых формул: в формулах Келлога и (6) вклад падает
пропорционально
в многокомпонентной
системе ее вклад в суммарную теплоту смешения зависит от вида используемых формул: в формулах Келлога и (6) вклад падает
пропорционально 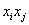 , в формулах Люписа
пропорционально
, в формулах Люписа
пропорционально 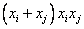 , в формулах Михайлова –
пропорционально
, в формулах Михайлова –
пропорционально 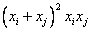 . Таким образом, при
разбавлении в формулах Келлога и (6) вклад сохраняется (и
стремится к регулярному), а в формулах Люписа (а, особенно, Михайлова) резко
снижается.Другими словами, последние формулы не позволяют описать (даже в качестве
частного случая) регулярное поведение бинарных систем в трех- и
многокомпонентных растворах!
. Таким образом, при
разбавлении в формулах Келлога и (6) вклад сохраняется (и
стремится к регулярному), а в формулах Люписа (а, особенно, Михайлова) резко
снижается.Другими словами, последние формулы не позволяют описать (даже в качестве
частного случая) регулярное поведение бинарных систем в трех- и
многокомпонентных растворах!
Это легко проиллюстрировать на примере гипотетической трехкомпонентной системы, в которой каждая бинарная система подчиняется регулярному поведению (а тройные взаимодействия отсутствуют – весьма тривиальный для ТРР случай). В этом случае получим:
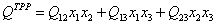 , (15)
, (15)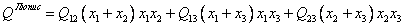 , (16)
, (16)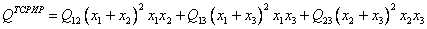 . (17)
. (17)Отличие формул очевидно даже внешне. Например, в точке
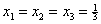 получим:
получим:
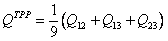 , (18)
, (18)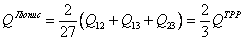 , (19)
, (19)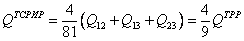 , (20)
, (20)т.е. 67 и 45% (менее половины) от требуемой! Получается, что в ТСРИР для описания регулярной тройной системы необходимо ввести несуществующее тройное взаимодействие, которое по величине больше двойного вклада в 1.25 раза. При увеличении разбавления (в многокомпонентных системах) ситуация становится вовсе катастрофической. Аналогичная ситуация наблюдается и с формулами Люписа (хотя и в несколько меньшей степени).
Нетрудно показать, что и в общем случае (2) и (3) остаются те же проблемы - резкое падение вклада двойных систем в суммарную теплоту смешения. Это приводит к необходимости учитывать тройные вклады, вводить существенно большие теплоты смешения в тройных системах, а, возможно, и к необходимости учета четверных взаимодействий и взаимодействий более высокого порядка.
3. Трехкомпонентные взаимодействия
Тройные взаимодействия в формулах ТСРИР имеют вид:
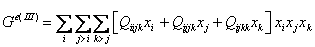 . (21)
. (21)Ситуация аналогична двойным системам – при разбавлении вклад тройной системы
уменьшается. Причина – в отсутствии в квадратных скобках свободного слагаемого
(без концентрации, т.е. отвечающего за трехчастичное взаимодействие 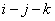 ).
).
4. Универсальные формулы перехода к трех- и многокомпонентным системам
Известны формулы Кохлера (см. [3], с. 256, уравнение (10.34)) для перехода от двойных систем к многокомпонентным:
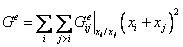 , (22)
, (22)где
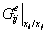 – энергия взаимодействия,
вычисленная для чистой двойной системы
– энергия взаимодействия,
вычисленная для чистой двойной системы
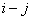 при
том же соотношении концентраций компонентов
при
том же соотношении концентраций компонентов
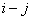 .
.
Интересно, но легко показать, что подстановка всех рассмотренных ранее формул дает идентичный результат – все получаемые формулы абсолютно одинаковы по виду зависимости от состава не только в бинарных, но и в многокомпонентных системах:
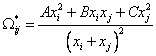 . (23)
. (23)Неудобство состоит в дробнорациональном виде и, как следствие, в существенном усложнении формул после дифференцирования (при расчете коэффициентов активности).
Известны также формулы Колинэ (см. [3], с. 256, уравнение (10.35)) для перехода от двойных систем к многокомпонентным:
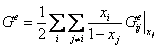 . (24)
. (24)Результаты подстановки всех рассмотренных ранее формул аналогичны формулам Кохлера – все получаемые формулы абсолютно одинаковы по виду зависимости от состава не только в бинарных, но и в многокомпонентных системах:
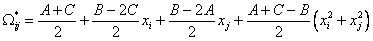 . (25)
. (25)Аналогичная ситуация (совпадение получаемых формул) сохраняется и в случае использования формул Кохлера и Колинэ для двухпараметрических моделей ТСР.
5.Вычисление параметров тройных систем
Вопросы выбора вида формул и физического смысла коэффициентов выходят за рамки данной статьи, поэтому ограничимся сравнением величин коэффициентов в различных моделях.
Оказывается, в первом приближении можно обойтись без повторного вычисления параметров по экспериментальным данным и для тройных систем, а вычислить их из имеющихся параметров. В качестве исходных данных используем полные формулы Михайлова [1, 2] (двойные и тройные вклады). Последовательность действий следующая:
- вычисляем параметры формул Келлога (3) для двойных систем по аналогичным параметрам Михайлова (см. выше);
- для тройных систем используем идентичное (21) выражение (но, естественно, коэффициенты будут другие):
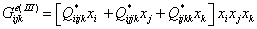 ; (26)
; (26) - записываем новые формулы в виде суммы формулы Келлога (3) для двойных вкладов и (26);
- приравниваем исходные формулы (для 3-х компонентной системы) к новым и вычисляем новые значения параметров
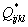 .
.
В результате получим следующие выражения для вычисления новых параметров:
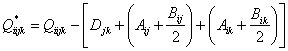 . (27)
. (27)Если для двойного вклада использовать формулы (6), то получим:
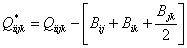 . (28)
. (28)При использовании формулы Люписа (2) получим:
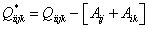 . (29)
. (29)И, наконец, при использовании формул Колинэ (25) получим:
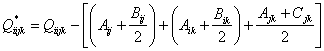 . (30)
. (30)Результаты пересчета для некоторых моделей приведены в таблице 2.
Интересно отметить следующее. При использовании формул Михайлова практически все параметры тройных систем отрицательные, среднее значение параметров очень большое (36.5 ккал) и имеет отрицательный знак. Это подтверждает предположение, что в тройных и многокомпонентных системах формулы Михайлова дают заниженный (по абсолютной величине) вклад двойных систем в суммарную энергию смешения и необходимо вводить большие (отрицательные) параметры тройных систем.

При использовании формул Келлога и (6) среднее арифметическое
значение существенно меньше (в 4 ÷ 6 раз). Идеальное (нулевое) значение
соответствует случаю, когда свойства тройных систем в среднем описываются
суммой двойных систем. Кроме того, снизились в 2 раза (в среднем) и абсолютные
значения параметров (от 43 до 22 ккал). Если посчитать количество параметров
одного знака, то у Михайлова получим 6 положительных и 62 отрицательных, в (6) – 50 и 51
соответственно. Все это свидетельствует о снижении необходимости учета тройных
вкладов в формулах Келлога и (6). Среднее значение тройного вклада в точке
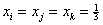 (где он практически максимальный) составляет у Михайлова 40 ккал, в (6) – 18 ккал. Это
приблизительно соответствует изменению коэффициента активности в 1.76 и 1.29
раза соответственно. Т.е. формулы Михайлова без учета тройных вкладов будут
работать с ошибкой вдвое большей, чем формулы Келлога и (6).
(где он практически максимальный) составляет у Михайлова 40 ккал, в (6) – 18 ккал. Это
приблизительно соответствует изменению коэффициента активности в 1.76 и 1.29
раза соответственно. Т.е. формулы Михайлова без учета тройных вкладов будут
работать с ошибкой вдвое большей, чем формулы Келлога и (6).
Почему это важно?
Если отсутствуют экспериментальные данные по некоторым системам, то более «качественными» будут формулы, у которых меньше необходимость учета вкладов тройных систем, т.е. такие, у которых в результате суммирования вкладов двойных систем получаются более близкие к эксперименту результаты. В этом и заключается основное преимущество формул Келлога и (6). Они позволяют более обоснованно использовать модель в тех тройных системах, по которым нет экспериментальных данных. Кроме того, появляется надежда, что в 4-х и многокомпонентных системах эти формулы будут давать более точные результаты (по аналогичной причине), особенно в системах с участием оксидов, по которым имеется ограниченное число экспериментальных данных.
Окончательные формулы (6) для коэффициента активности в многокомпонентных системах имеют вид:
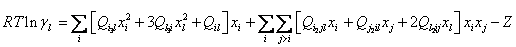 , (31)
, (31)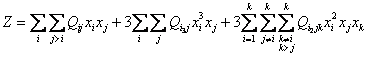 . (32)
. (32)где
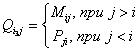 ,
,
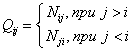 ,
,
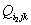 – обобщенное представление параметров
– обобщенное представление параметров
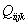 ,
,
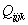 и
и
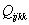 в виде одного трехмерного массива,
при этом
в виде одного трехмерного массива,
при этом
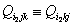 .
.
При совпадении любых двух индексов значение соответствующего параметра
тождественно равно нулю.
Следует отметить, что формулы (31)-(32) (с параметрами, рассчитанными по параметрам Михайлова) полностью идентичны (по результатам расчета теплот смешения и активностей компонентов) с исходными формулами Михайлова для бинарных и экспериментально исследованных трехкомпонентных систем! Отличие проявляется лишь в неизученных экспериментально тройных системах и, особенно, в многокомпонентных системах. Однако стремление получить полностью идентичные результаты расчета может быть не совсем корректно по двум причинам.
Во-первых, с точки зрения математической статистики более правильным является повторная обработка всех имеющихся экспериментальных данных с непосредственным определением новых значений параметров для выбранных формул.
Во-вторых, если рассмотреть исходные параметры Михайлова по тройным системам, то найдем 10 систем с нулевыми значениями параметров. Возможны два варианта интерпретации этого факта: отсутствие взаимодействия в этих системах (точнее, свойства этих систем прекрасно описываются суммой двойных вкладов, и нет необходимости учета вклада тройных систем), что маловероятно, если посмотреть на существенные величины тройных параметров по другим системам; либо просто отсутствуют экспериментальные данные по этим системам. В приведенном выше пересчете использован именно первый вариант (для достижения идентичности результатов), т.е. исходные параметры Михайлова считаются истинными по всем системам (даже если они нулевые), что приводит к появлению ненулевых параметров в формулах (6) для этих систем. Если же данные в действительности отсутствуют, то пересчет должен быть несколько другим: для тех тройных систем, по которым отсутствуют экспериментальные данные, должны быть приняты нулевые значения именно новых параметров в формулах (6).
Выводы
Таким образом, предлагаемый подход при выборе вида формул ТСР позволяет более обоснованно использовать модель в тройных и многокомпонентных системах, по которым нет (или имеется ограниченное число) экспериментальных данных.
Литература
- Михайлов Г.Г., Поволоцкий Д.Я. Термодинамика раскисления стали.– М.: Металлургия, 1993.– 82 с.
- Михайлов Г.Г., Чернова Л.А. Термодинамический анализ процессов раскисления коррозионностойкой стали Х18Н10Т кальцием и барием // Известия ВУЗов. Черная металлургия, 1991.- №12.-С. 37-40.
- Люпис К. Химическая термодинамика материалов. Пер. с англ. – М.: Металлургия, 1989. – 503 с.: ил.
- Kellog H.H. – In Phys. Chem. in Metallurgy / Ed. R.M. Fischer, R.A. Oriani, E.T. Turkdogan. – Monroeville: U. S. Steel Research Lab., 1976. P. 49-55 (ссылка из 3).
- Сабирзянов Т.Г. ТСР для металлических растворов.// Изв.вуз. Черная металлургия.- 1989.- N 1.- С. 1-4.
[1] -Полная таблица параметров приведена по данным: Михайлов Г.Г. Термодинамические принципы оптимизации процессов раскисления стали и модифицирования неметаллических включений. Дисс. докт. техн. наук. Москва, 1987.