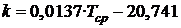(1)т.е. коэффициент нагрева металла растет с повышением температуры! На первый взгляд результат кажется абсурдным и абсолютно невозможным.
Для проверки было проанализировано изменение температуры между двумя замерами на 1730 плавках (всего 3470 экспериментальных точек). В качестве зависимой переменной использовалось отношение прироста температуры ΔT=T2-T1 к удельному расходу суммарной энергии ΔЕ (электрической и альтернативной), в качестве аргумента – средняя температура металла на интервале (Tср=(T1+T2)/2). В результате получили следующее уравнение регрессии (R=0,30) (рис. 1):
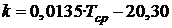(2)Невероятно, но результат практически идентичен формуле, заложенной изготовителем! Но ведь это противоречит самим основам теории теплообмена!
Возможной причиной может быть некорректная статистическая обработка, поскольку в выражении для зависимой переменной в знаменателе присутствует введенная между замерами энергия, что делает удельный вес точек с малым интервалом времени между замерами существенно выше. Однако обработка данных в виде зависимости прироста температуры от введенной энергии и средней температуры также дает положительный коэффициент при температуре (R=0,52):
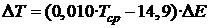(3)
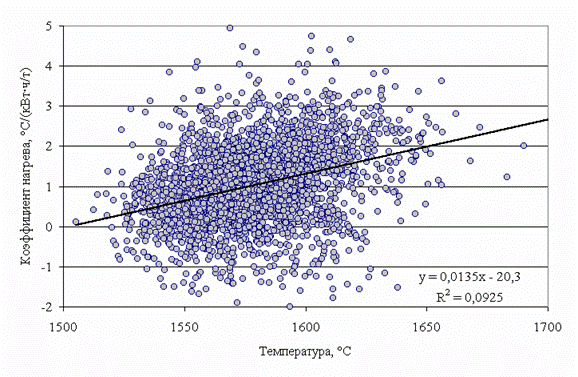
Рисунок 1. Зависимость коэффициента нагрева металла от средней температуры
Если взять в качестве аргумента начальную и конечную температуры металла на интервале, то получим следующие результаты (см. рис. 2, 3):
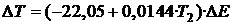(4)
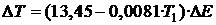(5)
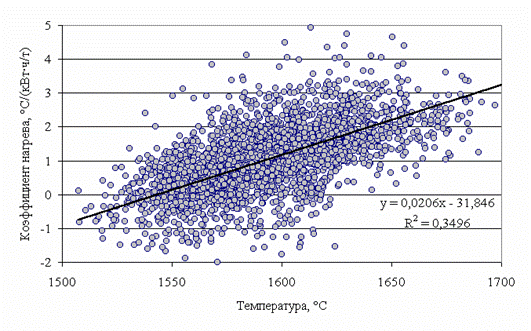
Рисунок 2. Зависимость коэффициента нагрева металла от конечной температуры
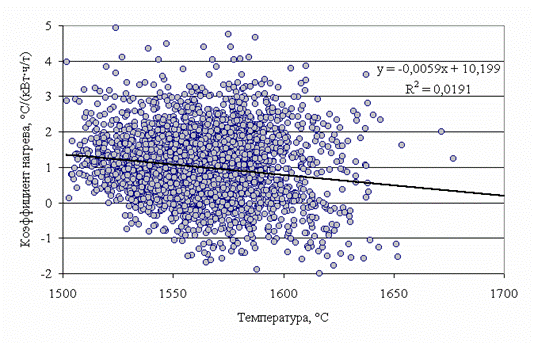
Рисунок 3. Зависимость коэффициента нагрева металла от начальной температуры
Полученные результаты позволяют сделать вывод, что положительное влияние температуры на нагрев металла на рис. 1 и 2 объясняется следующим. Обычно сталевар делает замер температуры после ввода определенного удельного количества энергии (на тонну лома) в печь, приблизительно соответствующего полному расплавлению металлозавалки (в среднем по массиву ранее проведенных плавок). Если при этом получена низкая температура, то это как правило связано с неполным расплавлением лома в результате неправильной информации о массе лома, простоя печи перед данной плавкой, неэффективной работы горелок или неэффективного электрического режима и т.д. В результате вводимое в дальнейшем тепло расходуется прежде всего на доплавление лома, а не на нагрев жидкой ванны, что сильно снижает коэффициент нагрева металла. Наоборот, более высокая температура при замере говорит о практически полном расплавлении металлозавалки, при этом все вводимое в дальнейшем тепло будет расходоваться в основном на нагрев ванны и даст более высокий коэффициент нагрева металла.
Следующий замер температуры
сталевар производит после отработки определенного количества энергии, которое
должно обеспечить нагрев ванны от первого замера до температуры выпуска (по
среднему коэффициенту нагрева металла на ранее проведенных плавках). В этом
случае при неполном расплавлении завалки на момент первого замера мы получим
низкую температуру второго замера и низкий коэффициент нагрева за счет малого
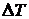, а при полном расплавлении – более высокую температуру
и более высокий коэффициент нагрева, т.е. изначально известна прямая пропорциональность k от T2.
Кроме того, использование «средней»(Tср) и конечной(T2)температуры для статистической обработки данных и последующего использования в модуле прогноза температуры абсолютно некорректно – после первого замера мы не знаем, какой будет следующий замер, и использовать можно только имеющуюся величину первого замера (т.е. T1).
Таким образом, в типичных условиях современной интенсивной технологии сталеварения по замеренной температуре невозможно однозначно определить (предсказать) ожидаемую скорость дальнейшего нагрева металла, поскольку здесь наблюдается взаимно противоположное влияние двух факторов: с одной стороны, чем выше температура замера, тем будут больше тепловые потери и меньше коэффициент нагрева; с другой стороны, чем выше температура замера, тем более полно расплавлена металлозавалка и можно ожидать более высокий коэффициент нагрева. Возможно, при высокой температуре преобладает влияние первого фактора (поскольку более вероятно полное расплавление металлозавалки), а при низкой – второго, однако определить эту границу не представляется возможным.
Необходима дополнительная информация, характеризующая состояние сталеплавильной ванны. Например, о полноте расплавления завалки можно судить по количеству энергии, введенной в печь к моменту первого замера температуры. Кроме того необходимо учесть, что тепловые потери растут с увеличением времени между замерами, т.е. интервал времени между замерами также должен быть включен в модель. Обработка данных в этом случае дает следующий результат (R=0,61):
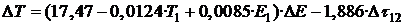(6)В формуле желательно также учесть продолжительность плавки (это влияет на
величину потерь тепла в период плавления), а также продолжительность межплавочного
простоя пустой печи, однако в рассмотренном массиве эти данные отсутствовали.Следует отметить, что был
использован практически «сырой» массив исходных данных, т.е. не
производились ни фильтрация недостоверных замеров, ни отсев плавок после длительных
простоев и т.д. Кроме того, в упрощенной модели не учитывалось влияние отдаваемых
шлакообразующих и моментов их отдачи (например, непосредственно перед замером).
Тем не менее, знаки и величины полученных коэффициентов не противоречат теоретическим положениям и практике сталеварения. Чем больше температура металла, тем меньше тепловой эффект от введенной энергии, что объясняется существенным повышением потерь излучением и теплопроводностью. Чем больше величина введенной энергии к моменту первого замера, тем меньше осталось в ванне нерасплавленного лома, тем лучше прогрета футеровка, что приводит к повышению коэффициента использования тепла непосредственно на нагрев жидкой ванны. И наконец, время между замерами увеличивает потери тепла – падение температуры металла при простое составляет около 2 ºC за минуту, что по порядку величины соответствует реальным данным.
Таким образом, предложенный алгоритм позволяет ориентировочно оценить ожидаемую скорость нагрева металла в ДСП и с приемлемой точностью прогнозировать текущую температуру сталеплавильной ванны.
Список литературы:
1. Об оценке температурной неоднородности ванны сталеплавильного агрегата. Скрябин В.Г., Скрябин Д.В., Кучеренко О.Л., Старосоцкий А.В., Храпко С.А. Теория и практика металлургии, 2004. – № 6. – С. 18-21.
2. Модель расчета средней температуры металла сверхмощной ДСП и ее применение в АСУТП. В.Г. Скрябин, Д.В. Скрябин. Материалы 2-й международной научно-практической конференции «Автоматизированные печные агрегаты и энергосберегающие технологии в металлургии» (3—5 декабря 2002 г.,г. Москва). — М.: МИСиС — С. 466-468.