Введение
При создании АСУТП выплавки и внепечной обработки стали центральную роль играют термодинамические модели взаимодействия компонентов расплава в сталеплавильной ванне. «Качество» термодинамических моделей, т.е. их способность адекватно описывать распределение элементов между взаимодействующими фазами (металл, шлак, газ и др.) в первую очередь зависит от точности использованных при их построении уравнений состояния фаз.Индивидуальность любой фазы определяется именно её уравнением состояния, из которого могут быть получены все термодинамические свойства фазы в результате соответствующих математических преобразований.
Состояние вопроса
Одним из основных вопросов термодинамики растворов является нахождение приближённого вида уравнения состояния. В большинстве случаев все известные теории статистической термодинамики растворов можно разделить по признаку практического использования на два класса: «сложные» теории, учитывающие многочисленные «тонкие» эффекты взаимодействия компонентов и приводящие, как правило, к математически сложным расчётным формулам и необходимости экспериментального определения большого числа эмпирических параметров даже для бинарных растворов; и упрощённые модели, часто вводимые формально, требующие ограниченного числа подгоночных параметров и обладающие разумной вычислительной сложностью. Теории первой группы по приведенным выше причинам не получили широкого распространения, модели второй группы приводят обычно к различного вида полиномиальным зависимостям и к невысокой точности аппроксимации экспериментальных данных [1,2].
Использование полиномиальных моделей (типа нулевого приближения теории регулярных растворов и её различных модификаций и усложнений) связано с ещё одной проблемой. Дело в том, что указанные модели обычно достаточно точно (с практической точки зрения) описывают интегральные термодинамические функции смешения, однако дают зачастую принципиально неверный ход кривых зависимости парциальных функций (например, активностей компонентов) от состава раствора. Последнее связано с тем, что на зависимостях интегральных функций фазы от состава на некоторых участках могут существовать незначительные отклонения от относительно плавного поведения этой зависимости на остальных участках. Природа и физическая сущность этих отклонений может быть различна, однако они приводят к тому, что на зависимостях парциальных свойств от состава появляются участки относительно резкого изменения этих свойств, при плавном поведении на остальных участках. В то же время простые полиномиальные модели либо дают плавные зависимости, либо требуют существенного повышения степени полинома, что неприменимо для практического использования в случае многокомпонентных растворов.
Наглядным примером таких зависимостей являются «интегралообразные» зависимости коэффициентов активности компонентов многих бинарных металлических систем от состава фазы, или коэффициента активности серы в оксидном (шлаковом) расплаве при изменении основности шлака [2,3]. Для описания такого хода парциальных свойств предлагались различные модели, например, «квадратичный формализм» Даркена [4], полимерные модели [5] и другие, однако они не получили широкого распространения.
Одной из возможных причин таких «особенностей» на зависимостях интегральных термодинамических свойств фазы от состава могут быть мезофазные переходы [6]. Известно, что жидкость имеет определённую микроструктуру («ближний порядок»), т.е. упорядоченность (симметрию) атомов в некоторых микроскопических пределах. Размеры упорядоченных областей в жидкости не превышают десятков или сотен атомов, в отличие от твёрдых кристаллов, обладающих макроскопической упорядоченностью (т.н. «дальний порядок»). Мезофазные переходы определяются сосуществованием в жидкости некоторых взаимно нерастворимых структур, обычно соответствующих устойчивым конденсированным фазам (например, структурам чистых компонентов). Изменение состава фазы приводит к изменению соотношения долей различных структур и, вследствие различия термодинамических свойств таких структур, в некоторых случаях может приводить к существенному «скачкообразному» изменению парциальных термодинамических (а также физических) свойств фазы.
Сосуществование различных структур (мезофаз) обычно связывается с флуктуациями состава и энергии, при этом роль флуктуаций энергии является преобладающей [6]. Флуктуационный подход к природе мезофаз позволяет истолковать существование различных структур статистически, т.е. образование, распад или переход в другое состояние происходит случайно (хаотически) в различных частях объёма фазы, однако средние (во времени) величины долей различных структур и их соотношение остаются постоянными.
Статистический характер флуктуаций приводит к микроскопическим размерам областей, обладающих различной структурой, что даёт возможность применить общие термодинамические законы к их рассмотрению при вычислении термодинамических свойств раствора.
Структурный вклад в интегральные термодинамические функции
Рассмотрим
многокомпонентный раствор, в котором возможно существование группировок атомов
(кластеров) нескольких различных структур. Введём следующие обозначения:
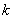 – число компонентов раствора;
– число компонентов раствора;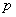 – число различных сортов кластеров;
– число различных сортов кластеров; 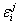 ,
,
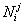 – потенциальная
энергия атома сорта
– потенциальная
энергия атома сорта 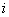 в структуре (кластерах) сорта
в структуре (кластерах) сорта 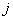 и суммарное число таких
атомов;
и суммарное число таких
атомов;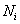 – общее число атомов сорта
– общее число атомов сорта 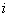 в фазе;
в фазе;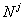 – общее число атомов всех сортов в структуре
– общее число атомов всех сортов в структуре 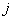 ;
;
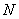 – общее число атомов всех сортов во всех
кластерах;
– общее число атомов всех сортов во всех
кластерах;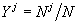 – мольная доля структуры
– мольная доля структуры 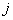 в фазе;
в фазе;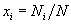
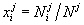 – мольная доля компонента
– мольная доля компонента
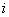 в фазе и в структуре
в фазе и в структуре 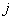 . Между ними имеются простые соотношения:
. Между ними имеются простые соотношения:
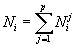 , ,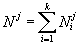 , ,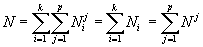 . . |
(1) |
В дальнейшем изложении считается (если не оговорено иначе), что перечисленные
ниже индексы могут принимать следующие значения: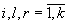 , а операции суммирования (если не оговорено иначе) также
производятся по всем возможным значениям индексов.
, а операции суммирования (если не оговорено иначе) также
производятся по всем возможным значениям индексов.
С учётом введенных обозначений получим:
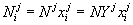 . . |
(2) |
Запишем
число способов осуществления распределения атомов при заданных значениях
величин 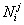 , которое определяется числом различимых перестановок атомов
(при отсутствии взаимодействия атомов внутри каждого кластера, т.е. в случае
неразличимости атомов определённого сорта в кластерах одного сорта). Если
кластеры существуют статистически (флуктуационно, т.е. «мерцают»), то получим:
, которое определяется числом различимых перестановок атомов
(при отсутствии взаимодействия атомов внутри каждого кластера, т.е. в случае
неразличимости атомов определённого сорта в кластерах одного сорта). Если
кластеры существуют статистически (флуктуационно, т.е. «мерцают»), то получим:
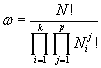 |
(3) |
Время нахождения системы в определённом состоянии определяется относительной вероятностью реализации этого состояния, поэтому практически всегда имеет место наиболее вероятное распределение, осуществляемое наибольшим числом способов при постоянстве состава и энергии системы. В изобарно-изотермических условиях можно также воспользоваться критерием минимума энергии Гиббса, что идентично по результатам, однако существенно лаконичнее. Проделаем необходимые для этого преобразования.
Запишем энтропию раствора, используем формулу Стирлинга и подставим (2):
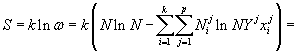 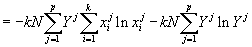 . . |
(4) |
Переходя к 1 молю раствора, получим мольную энтропию раствора:
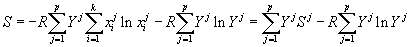 , , |
(5) |
где 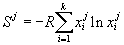 – мольная энтропия
кластеров сорта
– мольная энтропия
кластеров сорта 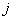 (идеальная).
(идеальная).
Первое слагаемое в (5) есть обычная сумма энтропии всех возможных кластеров разных сортов с учётом их относительных количеств, а второе определяет дополнительное изменение энтропии, которое можно формально трактовать как энтропию перестановки кластеров между собой.
Запишем выражение для энергии раствора. Очевидно, что она складывается из энергий отдельных атомов, тогда
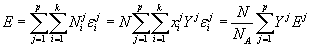 , , |
(6) |
где 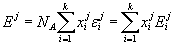 – энергия 1 моля
кластеров сорта
– энергия 1 моля
кластеров сорта 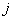 ;
;
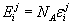 – энергия 1 моля атомов сорта
– энергия 1 моля атомов сорта 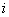 в кластерах сорта
в кластерах сорта 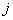 .
.
Переходяк 1 молю раствора, получим:
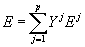 . . |
(7) |
Из (5) и (7) получим выражение для мольной энергии Гиббса раствора:
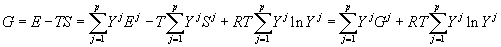 , , |
(8) |
где 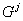 – мольная энергия Гиббса структуры
– мольная энергия Гиббса структуры 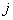 .
.
Таким образом, термодинамические свойства фазы определяются аддитивной суммой соответствующих свойств сосуществующих структур с учётом относительных количеств (долей) каждой из них и дополнительной энтропией перестановки кластеров различной структуры, численно равной энтропии идеального раствора, компонентами которого являются кластеры различных структур (мезофазы).
Флуктуационные кластеры одинакового состава
Если флуктуации энергии имеют подавляющее преобладание по сравнению с флуктуациями
состава, то это приводит к тому, что все мезофазы имеют одинаковый (тождественный)
состав, совпадающий с составом раствора (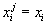 )
, но отличающиеся потенциальные энергии. В этом случае для
любых
)
, но отличающиеся потенциальные энергии. В этом случае для
любых 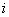 и
и 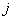 имеем:
имеем:
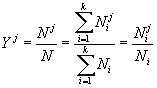 , , 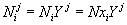 , , |
(9) |
тогда из (5) получим:
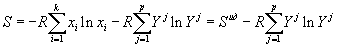 . . |
(10) |
Очевидно, что первое слагаемое есть идеальная энтропия смешения компонентов при отсутствии структурных эффектов, а второе – структурный вклад в энтропию раствора, численно равный идеальной энтропии перестановки кластеров различных структур, т.е. для структурного вклада в мольные термодинамические функции раствора можно записать:
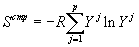 , , 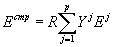 , , |
(11) |
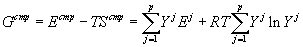 . . |
(12) |
В формулах (11) – (12) остались неизвестными величины 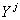 , определяющие распределение атомов по кластерам различного
сорта. Как уже отмечалось, их можно найти из критерия минимума энергии Гиббса.
В качестве дополнительного ограничения необходимо указать следующее условие
материального баланса:
, определяющие распределение атомов по кластерам различного
сорта. Как уже отмечалось, их можно найти из критерия минимума энергии Гиббса.
В качестве дополнительного ограничения необходимо указать следующее условие
материального баланса:
 . . |
(13) |
Запишем функцию Лагранжа:
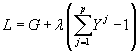 , , |
(14) |
где 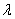 – неопределенный
множитель Лагранжа.
– неопределенный
множитель Лагранжа.
Дифференцируя 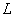 по
по 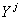 и приравнивая
производные нулю, получим:
и приравнивая
производные нулю, получим:
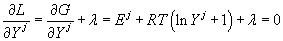 , , |
(15) |
откуда
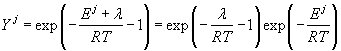 . . |
(16) |
Из (16) и (13) несложно найти, что средняя суммарная мольная доля кластеров определённой структуры пропорциональна фактору Больцмана:
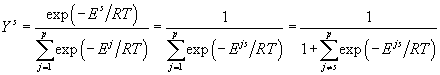 , , |
(17) |
где 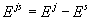 – изменение
потенциальной энергии 1 моля раствора при переходе из структуры
– изменение
потенциальной энергии 1 моля раствора при переходе из структуры 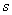 в структуру
в структуру 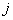 ,
,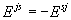 .
.
Если структуру 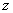 выбрать в качестве
«базовой», относительно которой будут рассматриваться все остальные, то
получим:
выбрать в качестве
«базовой», относительно которой будут рассматриваться все остальные, то
получим:
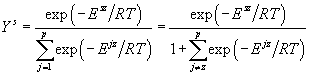 |
Очевидно, что
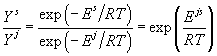 . . |
(18) |
Из (17) или (18) следует, что
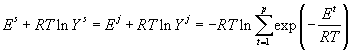 . . |
(19) |
Подставляя (17) в (12), получим:
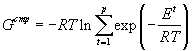 . . |
(20) |
Подставляя (19) в (12) или (20), получим
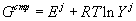 , , 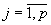 . . |
(21) |
Дифференцирование выражений (20) или (21) по температуре дает исходные формулы (11), как и требуется с точки зрения формальной термодинамики.
Последними величинами, оставшимися неопределёнными в полученных формулах, являются энергии
кластеров различного сорта 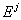 , которые в принципе могут быть любыми функциями состава
кластеров (т.е. состава раствора) и температуры.
, которые в принципе могут быть любыми функциями состава
кластеров (т.е. состава раствора) и температуры.
В первом приближении можно считать, что энергии 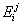 атомов сорта
атомов сорта 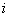 в кластерах сорта
в кластерах сорта 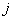 постоянны и не зависят от состава и температуры. В этом случае уравнение (21) приобретает очень простой вид
после отбрасывания аддитивной составляющей
постоянны и не зависят от состава и температуры. В этом случае уравнение (21) приобретает очень простой вид
после отбрасывания аддитивной составляющей 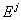 :
:
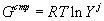 . . |
(22) |
Для вычисления функции смешения необходимо из формул (20) – (22) вычесть аддитивную составляющую, равную сумме произведений мольных долей компонентов раствора на энергию Гиббса (вычисленную по той же формуле) в точках чистых компонентов:
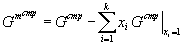 . . |
(23) |
Примеры зависимостей термодинамических функций от состава раствора приведены на рис. 1.
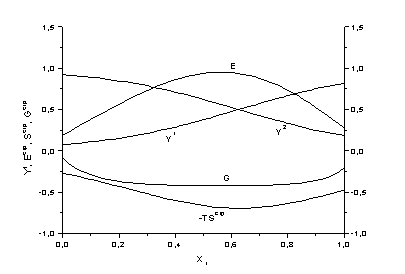 | |
Рис.1. Зависимость 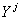 , ,
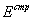 , ,
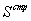 и и
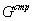 от состава раствора
для флуктуационных кластеров одинакового состава (энергетические параметры
приведены в единицах от состава раствора
для флуктуационных кластеров одинакового состава (энергетические параметры
приведены в единицах 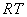 |
Необходимо отметить, что предположение об отсутствии взаимодействия атомов в кластерах использовано лишь для упрощения изложения при выводе формул (3) – (23). Можно показать, что выражения (11) – (23) сохраняются и в случае любого взаимодействия частиц раствора, т.е. при неидеальности поведения атомов в кластерах. Более того, предположение об одинаковости взаимодействия атомов в кластерах также не является обязательным. Единственно необходимым и существенно важным является лишь то, что они имеют одинаковый состав, совпадающий с составом раствора. В общем случае уравнения для мольной свободной энергии раствора и мольной доли кластеров имеют следующий вид:
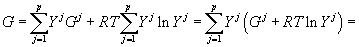
|
(24) |
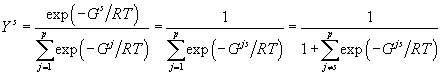 , , |
(25) |
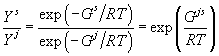 , , |
(26) |
где 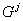 – мольная энергия
Гиббса структуры
– мольная энергия
Гиббса структуры 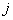 ;
;
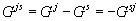 – изменение энергии
Гиббса 1 моля раствора при переходе из структуры
– изменение энергии
Гиббса 1 моля раствора при переходе из структуры 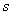 в структуру
в структуру
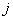 .
.
Формулы для вычисления энтропии и энтальпии раствора легко получить, продифференцировав выражение (24) по температуре, при этом получаемые зависимости совпадают с (5) и (7), как и требуется с точки зрения формальной термодинамики.
Для практического использования полученных формул необходимо задать вид зависимости
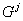 от состава кластеров.
В первом приближении можно принять, что мольные термодинамические потенциалы
мезофаз отличаются друг от друга на постоянные величины начального уровня
отсчёта энергии, характерные для каждой мезофазы, при одинаковых потенциалах
смешения.
от состава кластеров.
В первом приближении можно принять, что мольные термодинамические потенциалы
мезофаз отличаются друг от друга на постоянные величины начального уровня
отсчёта энергии, характерные для каждой мезофазы, при одинаковых потенциалах
смешения.
В этом случае для мольной энергии Гиббса получим:
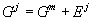 , , |
(27) |
где 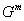 – потенциал смешения
(без учёта структурного вклада).
– потенциал смешения
(без учёта структурного вклада).
Подстановка (27) в (24) дает следующую формулу:
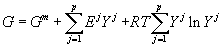 , , |
(28) |
где первое слагаемое есть изменение энергии Гиббса при смешении компонентов без учёта «структурной» составляющей, а остальные слагаемые – дополнительный «структурный» вклад, обусловленный мезофазным переходом (изменением структуры расплава):
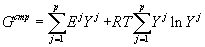 , , |
(29) |
что полностью совпадает с (12).
Флуктуационные кластеры произвольного состава
Если в жидкости помимо флуктуаций энергии, наблюдаются флуктуации состава и они имеют
достаточную величину, то возможно образование «мерцающих» (флуктуационных, т.е.
существующих статистически) кластеров произвольного состава, отличающихся друг
от друга не только энергией (например, за счёт различной симметрии или упорядочения),
но и составом за счёт перераспределения атомов между кластерами из-за отличающихся
энергий атомов в кластерах различных сортов. Другими словами, атомы определённого
сорта будут переходить преимущественно в те кластеры, в которых их энергия минимальна.
В этом случае условие тождественности состава кластеров отсутствует
(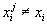 ). В результате аналогичных выкладок для энергии Гиббса фазы
получим:
). В результате аналогичных выкладок для энергии Гиббса фазы
получим:
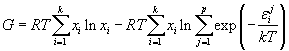 . . |
(30) |
Второе слагаемое в (30) линейно зависит от состава фазы, поэтому для мольной энергии Гиббса смешения получим величину, совпадающую с энергией Гиббса идеального раствора:
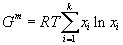 , , |
(31) |
т.е. без какого-либо структурного вклада. Составы кластеров при изменении состава фазы меняются таким образом, что «съедают» второе слагаемое в выражении (10)(структурный вклад в энтропию фазы).
Расслоение на отдельные фазы
Рассмотренный выше случай и полученные формулы очень похожи на ситуацию расслаивающейся фазы (или двухфазного равновесия), поскольку в последнем случае также мольные доли кластеров (или фаз) линейно изменяются при изменении интегрального состава фазы (системы). Воспользовавшись тем же методом, получим следующие зависимости:
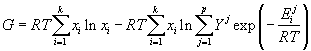 . . |
(32) |
Величины мольных долей кластеров (фаз) 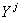 рассчитываются по формулам:
рассчитываются по формулам:
 . . |
(33) |
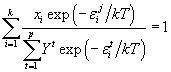 , ,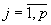 . . |
(34) |
Аналитическое решение системы (34) для двухкомпонентной (1 и 2)
двухструктурной (двухфазной, 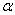 и
и 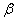 )
жидкости и подстановка его в (33) и (32) показывает, что при изменении
состава системы составы кластеров (фаз) неизменны, а мольные доли структур
линейно зависят от состава, при этом полученные значения
)
жидкости и подстановка его в (33) и (32) показывает, что при изменении
состава системы составы кластеров (фаз) неизменны, а мольные доли структур
линейно зависят от состава, при этом полученные значения 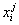 соответствуют точкам, в которых мольные доли соответствующих им структур
соответствуют точкам, в которых мольные доли соответствующих им структур 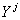 равны единице.
Двухфазное равновесие соблюдается в интервале между
равны единице.
Двухфазное равновесие соблюдается в интервале между 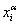 и
и 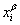 , в котором
, в котором 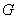 системы линейно зависит
от состава системы, а за пределами этого интервала
системы линейно зависит
от состава системы, а за пределами этого интервала 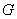 системы совпадает с
системы совпадает с  соответствующей чистой
фазы. Очевидно, что в случае однофазной системы состав присутствующей фазы совпадает
с составом системы.
соответствующей чистой
фазы. Очевидно, что в случае однофазной системы состав присутствующей фазы совпадает
с составом системы.
Устойчивые кластеры произвольного состава
Для полноты анализа рассмотрим также случай существования в растворе устойчивых (т.е. «долгоживущих») кластеров. Такая ситуация возможна, если образующиеся кластеры не обладают взаимной межфазной энергией. В этом случае кластеры различного сорта имеют произвольные составы, отличающиеся друг от друга и от интегрального состава фазы (за счёт перераспределения атомов между кластерами), однако кластеры одного сорта, естественно, имеют одинаковый состав. В общем случае все кластеры имеют разные (произвольные) размеры.
Если провести аналогичные выкладки, то получим формулы, полностью совпадающие с ситуацией расслоения на отдельные фазы (в т.ч. имеющиеся ограничения), поэтому все получаемые результаты анализа абсолютно идентичны уравнениям (32) – (34) и не дают ничего нового. Другими словами, устойчивые кластеры представляют собой (в термодинамическом плане) диспергированный вариант расслоения системы на отдельные («чистые») структуры, что и приводит к аналогичным зависимостям термодинамических свойств от состава.
Сравнение и анализ полученных формул
Выше получены три варианта поведения термодинамических свойств раствора:
- Существование флуктуационных кластеров одинакового состава.
- Существование флуктуационных кластеров произвольного состава.
- Существование устойчивых кластеров произвольного состава или расслоение на «чистые» структуры (фазы).
Примеры зависимости энергии Гиббса системы от интегрального состава системы для всех вариантов приведены на рис.2. Проанализируем физические предпосылки каждого из вариантов и полученные для них формулы.
- С точки зрения величины энергии Гиббса раствора:
По сравнению с расслоением раствора на «чистые» фазы или устойчивыми кластерами произвольного состава, образование флуктуационных кластеров всегда энергетически выгодно, поскольку даёт дополнительный вклад в энтропию смешения за счёт перестановки кластеров между собой, поэтому 1-й и 2-й варианты имеют меньшую энергию Гиббса, чем вариант 3.
Появление кластеров произвольного состава в растворе приводит к перераспределению компонентов между кластерами за счёт различных энергий (хим. потенциалов) этих компонентов в разных кластерах (обладающих отличающимися уравнениями состояния), что приводит к формулам варианта 2. Наличие в этом случае дополнительных степеней свободы в виде составов кластеров приводит к меньшей энергии Гиббса (наименьшей из всех рассмотренных вариантов) в варианте 2, чем в варианте 1. Составы кластеров изменяются таким образом, чтобы получить наименьшую энергию Гиббса, которая достигает минимально возможной величины в данных условиях, т.е. величины идеальной энергии Гиббса (структурный вклад в функцию смешения при этом становится равным нулю), поэтому выражение для свободной энергии смешения в варианте 2 полностью совпадает с аналогичным выражением для идеального раствора и не даёт ничего принципиально нового по сравнению с имеющимися зависимостями, т.е. существуют такие кластеры или нет – в выражении для
 это никак не отражается.
это никак не отражается.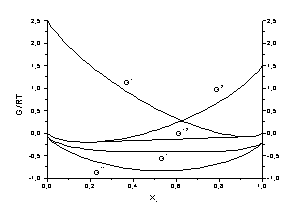
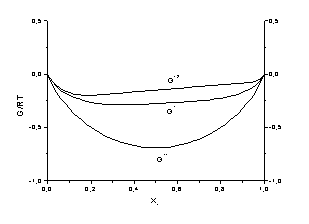
a) б) Рис.2. Энергия Гиббса для всех рассмотренных случаев (пример). Интегральные функции (а) и функции смешения (б):
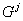 – чистая структура
– чистая структура 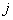
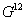 – двухфазная система
(или устойчивые кластеры произвольного состава);
– двухфазная система
(или устойчивые кластеры произвольного состава); 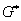 – флуктуационные
кластеры одинакового состава;
– флуктуационные
кластеры одинакового состава; 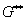 – флуктуационные кластеры
произвольного состава (совпадает с идеальной).
– флуктуационные кластеры
произвольного состава (совпадает с идеальной). -
С точки зрения возможности одновременного сосуществования различных кластеров в растворе:
Образование «долгоживущих» или «короткоживущих» кластеров и их одновременное сосуществование в растворе возможно лишь в том случае, если образующиеся структуры не обладают межфазным натяжением (т.е. неограниченно взаимно растворимы). В противном случае (взаимная нерастворимость) появляющаяся поверхностная энергия существенно превышает выигрыш в энтропии смешения и делает невозможным сосуществование таких кластеров, приводя к распаду (расслоению) на две (или более) «чистых» фаз (т.е. к варианту 3), с более высокой энергией Гиббса.
-
С точки зрения величины флуктуаций энергии и состава:
Незначительная величина флуктуаций состава приводит к тому, что реализация варианта 2 становится весьма сомнительной. Возможно, что чем меньше и подвижнее атомы и выше температура, тем более вероятно осуществление варианта 2 (при этом термодинамические свойства раствора приближаются к идеальному поведению).
В то же время существование флуктуаций энергии и их значительное преобладание над флуктуациями состава делает возможным существование «мерцающих», т.е. «короткоживущих» кластеров, обладающих одинаковым составом, но отличающейся энергией (например, за счёт изменения симметрии). Такие кластеры не вызывают появления межфазного натяжения, поскольку они обладают одинаковым составом, поэтому такая фаза является более выгодной в термодинамическом отношении, чем двухфазная система.
В дальнейшем изложении рассматривается именно существование кластеров одинакового состава. Статистический характер распределения энергии между кластерами приводит к «интегралообразным» зависимостям избыточных парциальных термодинамических функций, что соответствует многочисленным экспериментально наблюдаемым зависимостям физико-химических свойств многих растворов от состава фазы.
Структурный вклад в коэффициенты активности компонентов раствора
Для практического использования полученных формул необходимо задать вид уравнений зависимости потенциальной энергии кластеров каждой структуры от их состава (т.е. состава раствора).
В первом приближении примем линейную зависимость:
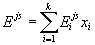 . . |
(35) |
где 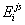 – эмпирические коэффициенты (параметры модели), определяемые из экспериментальных данных.
– эмпирические коэффициенты (параметры модели), определяемые из экспериментальных данных.
Общее число параметров составляет 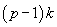 .
В случае учёта только двух структур необходимое количество
параметров равно числу компонентов раствора (обычно элементов Периодической
системы).
.
В случае учёта только двух структур необходимое количество
параметров равно числу компонентов раствора (обычно элементов Периодической
системы).
Дифференцирование выражений (20) – (23) даёт формулы для вычисления парциальных энергий Гиббса, т.е. структурного вклада в химические потенциалы компонентов раствора, в этом случае для коэффициентов активности получим:
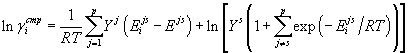 . . |
(36) |
Анализ полученных формул в случае двух структур
Рассмотрим многокомпонентную фазу, в которой могут существовать две структуры
(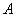 и
и 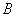 ).
В этом случае получим следующие расчётные формулы:
).
В этом случае получим следующие расчётные формулы:
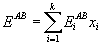 , , |
(37) |
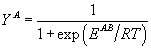 , , 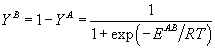 , , |
(38) |
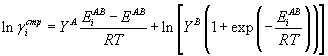 . . |
(39) |
Рассматривая (39) в пределе при 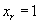 получим коэффициент активности компонента
получим коэффициент активности компонента 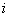 при бесконечном разбавлении в компоненте
при бесконечном разбавлении в компоненте 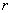 :
:
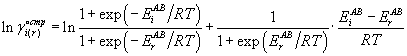 . . |
(40) |
Анализ формулы (40) показывает, что структурный вклад
всегда приводит к увеличению положительного отклонения от идеального поведения
раствора, а рассматривая (40) в пределе при 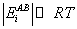 ,
,
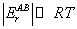 , получим, что при бесконечном разбавлении структурный вклад
в коэффициент активности приближённо равен (особенно при больших абсолютных
значениях параметров
, получим, что при бесконечном разбавлении структурный вклад
в коэффициент активности приближённо равен (особенно при больших абсолютных
значениях параметров 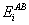 ,
,
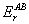 )
энергетическому эффекту (по модулю) перехода атомов сорта
)
энергетическому эффекту (по модулю) перехода атомов сорта 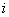 из энергетически менее выгодной структуры в более выгодную.
из энергетически менее выгодной структуры в более выгодную.
Использование модели при описании оксидных и солевых расплавов
Полученные выше формулы без изменений могут быть использованы при описании оксидных и солевых
систем, однако если элементами теплового движения принимать не соединения, а
атомы, составляющие фазу (т.е. компонентами считать элементы Периодической
системы), то формулы принимают несколько иной вид, поскольку в электронейтральной
фазе концентрация одного из компонентов является зависимой переменной. В
качестве «зависимого» компонента удобнее всего выбрать кислород, всегда присутствующий
в оксидных фазах. В этом случае для оксидной фазы, в которой могут существовать
две структуры (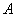 и
и 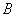 )
, получим следующую формулу:
)
, получим следующую формулу:
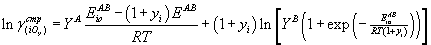 , , |
(41) |
где 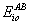 – эмпирические
параметры, определяемые из экспериментальных данных;
– эмпирические
параметры, определяемые из экспериментальных данных; 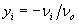 – стехиометрический коэффициент кислорода в соединении
– стехиометрический коэффициент кислорода в соединении 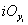 ;
;
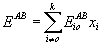 .
.
Для серы в случае двух структур получим очень простое выражение:
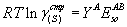 , , |
(42) |
Результаты статистической обработки литературных экспериментальных данных по сульфидной емкости шлака и равновесному распределению серы между металлом и шлаком [3,7] приведены в табл. 1 и 2.
Таблица 1. Расчетные величины параметров модели.
|
|
S |
Fe |
Mn |
Ca |
F |
Mg |
Al |
Si |
|
|
37.8 |
57.1 |
38.3 |
17.4 |
12.8 |
9.4 |
-8.1 |
-21.0 |
Таблица 2. Статистические параметры
выборки (254 точки) для 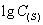
|
Величина |
Учет структурного вклада |
|
|
нет |
есть |
|
|
Остаточная сумма квадратов |
250.7 |
9.7 |
|
Стандартное отклонение |
1.0157 |
0.199 |
Достигнутая точность прогнозирования равновесного распределения серы между металлом и шлаком (см. табл. 2 и рис. 3) позволяет использовать предложенную модель для практических расчетов. Для описания активностей всех остальных компонентов шлака наилучшую точность предсказания показала теория субрегулярных ионных растворов Г.Г. Михайлова [8], что и определило ее выбор в качестве «базовой» модели.
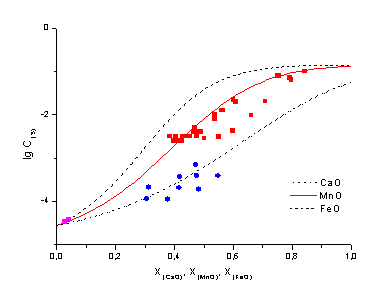 | |
Рис.3. Влияние состава шлака на коэффициент активности серы в бинарных системах
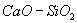 , ,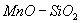 , ,
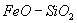 . Точки – экспериментальные данные. . Точки – экспериментальные данные. |
Выводы
- Проведенный анализ показал возможность объяснения «интегралообразного» поведения активностей компонентов на основе рассмотрения мезофазных переходов, происходящих в жидких растворах.
- Получены конечные формулы, пригодные для использования в практических расчетах коэффициентов активности компонентов металлических и шлаковых фаз.
- В результате статистической обработки экспериментальных данных получены параметры модели для расчета коэффициента активности серы в оксидных шлаках.
- Разработанная модель внедрена в состав АСУТП выплавки и внепечной обработки стали «ОРАКУЛ» в составе комплексной АСУТП ЭСПЦ Молдавского металлургического завода, что позволило существенно повысить точность прогноза содержания серы в металле.
Библиографический список
- Люпис К. Химическая термодинамика материалов. Пер. с англ. – М.;: Металлургия, 1989. – 503 с.: ил.
- Григорян В.А., Белянчиков Л.Н., Стомахин А.Я. Теоретические основы электросталеплавильных процессов. – М.: Металлургия, 1987. – 272 с.: ил.
- Эллиот Д.Ф., Глейзер М., Рамакришна В. Термохимия сталеплавильных процессов. – М.: Металлургия, 1969. – 252 с.: ил.
- Darken L.S. // Trans. Of Metall. Soc. AIME. 1967. V. 239. P. 90-96.
- Есин О.А. Константа образования и строение силикатных полимеров. // ЖФХ. – 1978. – т. 52. – ╧ 4. – С. 1073-1074.
- Семенченко В.К. Устойчивость, флуктуации и фазовые переходы. // В кн.: Перегретые жидкости и фазовые переходы. Свердловск: УНЦ АН СССР. – 1979. – С. 3-21.
- Sigworth G.K., Elliott J.F. The Thermodynamics of Liquid Dilute Iron Alloys // Met. Sci. – 1974. – V.8. – P. 298-310.
- Михайлов Г.Г. Термодинамические принципы оптимизации процессов раскисления стали и модифицирования неметаллических включений. Дисс. докт. техн. наук. Москва, 1987.
© С.А. Храпко, 2004
| Вверх |
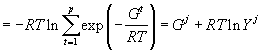 ,
,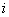
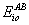 , ккал/моль
, ккал/моль