| Публикации: | АСУТП | Теория и технология | Научные работы | Главная |
«Прогрессивные технологии непрерывной разливки: XXI век»
28—31 мая 2002, г. Донецк
Рассмотрены вопросы построения моделей для создания автоматизированных систем управления технологическими процессами выплавки и обработки стали в металлургических агрегатах, такие как выбор критериев равновесия, выбор уравнений состояния металла и шлака, учет кинетических сдвигов от термодинамического равновесия, расчет гидродинамики сталеплавильного агрегата.
Наличие автоматизированных систем управления технологическими процессами (АСУТП) становится нормой в современном сталеплавильном производстве. В то же время, круг задач, решаемых этими системами, часто ограничен автоматизацией элементарных технологических операций, информационным сопровождением процессов и статистической обработкой данных. Построение эффективных систем управления без решения этих задач, конечно, немыслимо, но возможности современных науки, аппаратных и программных средств гораздо шире.
Потребности современного производства и возможности металлургической науки ставят задачу оперативного (модно звучит – «в режиме реального времени») моделирования процессов выплавки и обработки стали и сталеплавильного производства в целом системами управления.
Одна из актуальных задач в сталеварении – прогнозирование химического состава и температуры металла. Именно адекватный прогноз позволяет эффективно решать задачи непосредственного управления, а также весь круг сопутствующих задач, предназначенных для повышения эффективности работы металлургического агрегата, цеха и предприятия в целом.
Построение системы управления, умеющей осуществлять прогноз химического состава и температуры металла, вряд ли возможно без использования результатов теоретических исследований в термодинамике и кинетике.
Основу системы прогнозирования составляет термодинамический расчет равновесного состава. Стоит учесть, что это, пожалуй, единственный известный строго доказанный факт. Для реализации этого подхода необходимо определить критерии равновесия; выбрать уравнения состояния фаз; построить схему решения системы уравнений.
В литературе со ссылкой на Гиббса критерии равновесия выводятся следующим образом. Утверждается, что равновесному состоянию закрытой многофазной системы соответствуют экстремальные значения термодинамических потенциалов системы, например, минимум энергии Гиббса G при условии постоянства соответствующих термодинамических переменных (p и T) и выполнении уравнений материального баланса. Для практического использования этот критерий обычно записывают в виде производных, т.е. в терминах химических потенциалов. Считается, что такая постановка задачи является обычным поиском условного экстремума функции многих переменных при наличии уравнений связи между независимыми переменными (ограничений) в виде равенств, что приводит к использованию метода Лагранжа. В результате получают критерии равновесия в виде равенства во всех фазах температуры, давления и химических потенциалов компонентов, образующих замкнутую систему:
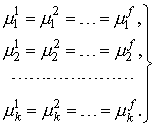| (1) |
Указанный ход рассуждений действительно принадлежит Гиббсу, однако практическое использование такого критерия требует некоторых дополнений.
Условие равенства химических потенциалов во всех фазах является достаточным, но не необходимым условием. Более точно указанные критерии равновесия необходимо сформулировать в следующем виде: если установилось состояние равновесия, то во всех образовавшихся фазах (и только в них) химические потенциалы будут равны. Обратное утверждение, вообще говоря, неверно – в системе уравнений с равенством химических потенциалов во всех возможных в данных условиях фазах решение может просто отсутствовать – система окажется несовместной.
В общем виде проблему можно сформулировать следующим образом. Чтобы найти равновесный состав системы (перечень фаз и количества каждого компонента в них), нужно записать (и затем решить) соответствующую систему уравнений. Но чтобы записать систему уравнений, необходимо знать фазовый состав системы, который станет известным лишь после нахождения равновесного состава системы, и который мы не знаем заранее.
Указанная проблема вовсе не порочит метод Гиббса или использованный метод Лагранжа. Дело в том, что Гиббс, рассматривая термодинамику как формальную схему, допускал отрицательные массы фаз. В этом случае система уравнений для любого набора фаз всегда будет иметь соответствующее решение (даже если в ответе будут фигурировать отрицательные массы).
В практических расчетах это недопустимо. Формальный анализ приведенной выше схемы рассуждений указывает на то, что при составлении функции Лагранжа пропущены условия неотрицательности масс компонентов в фазах (подразумевается, что это и так ясно):
 | (2) |
На самом деле, это такие же дополнительные условия (ограничения), как и условия материального баланса, только в виде неравенств, а не уравнений. Учет его в функции Лагранжа послевыполнения описанных выше преобразований приводит к следующей формулировке критериев химического равновесия:
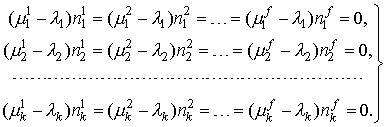 | (3) |
В отличие от (1), в систему уравнений (3) могут быть записаны абсолютно все фазы, существование которых возможно в данной системе, даже если это будет противоречить правилу фаз. В результате решения «лишние» фазы будут исключены из ответа (их массы станут равными нулю), при этом уравнения (3) останутся справедливыми и в ситуации отсутствия каких-либо компонентов или фаз: при строго нулевой массе компонента или фазы соответствующие уравнения становятся тождеством и автоматически исключаются из системы уравнений.
Таким образом, система уравнений (3) является более общим критерием равновесия, чем (1).
Недостаточность (1) проявляется и в других приложениях термодинамики. Например, в методе коллективизированных электронов (МКЭ) предлагается считать компонентами оксидных и солевых фаз химические элементы Периодической системы Менделеева, при этом для такой фазы автор добавляет условие электронейтральности (4):
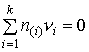 | (4) |
а на основе привлечения дополнительных предположений относительно физической природы шлака в уравнение химического потенциала компонента солевого раствора вводится дополнительное слагаемое (5):
 | (5) |
В действительности необходимость введения дополнительного слагаемого и дополнительных предположений относительно физической природы шлака отсутствует. Для этого достаточно учесть, что (4) является обычным дополнительным условием (ограничением), поэтому его необходимо включать в функцию Лагранжа наравне со всеми остальными ограничениями. В простейшем случае (система металл-шлак) получим формулу (6), т.е. формулы МКЭ:
 | (6) |
Таким образом, формулы
Уравнение состояния определяет индивидуальность любой фазы. Многолетний опыт решения практических задач позволил сделать следующий выбор. Термодинамическое состояние элемента в шлаке описывается с помощью теории регулярных ионных растворов В.А. Кожеурова и теории субрегулярных ионных растворов Г.Г. Михайлова с учетом дополнительного вклада энергии мезофазных переходов, что особенно актуально для корректного вычисления активности серы и фосфора в шлаке. Для расчета коэффициентов активности элементов металла выбрана теория субрегулярных растворов. В настоящее время это единственные надежные и широко доступные методы расчета активностей, обеспеченные численными значениями параметров.
К сожалению, пришлось отказаться от метода
коллективизированных электронов из-за крайне низкой точности расчета
активностей, и от метода параметров взаимодействия Вагнера, которые дают
принципиально неверный ход кривой активности в области повышенных концентраций,
не согласуются с уравнением
Поскольку одной из основных задач, которая ставилась в исследованиях – прогноз химического состава металла и температуры, то принято, что в сталеплавильных агрегатах основная масса всех поступающих веществ сосредотачивается в жидких металле и шлаке и в газовой фазе. Влияние других фаз (взаимодействие с футеровкой, выделение неметаллических включений (НВ), вынос пыли и т.д.) не оказывает существенного влияния на химический состав жидкого металла. Поэтому основным является расчет равновесия в системе металл-шлак-газ, а состав и количество НВ определяется дополнительным расчетом по результатам вычисления текущего состава металла и шлака.
Учёт кинетических сдвигов с использованием понятия «реакционной зоны» проводился с использованием следующих основных положений:
Расчет производится следующим образом:
В качестве примера вычисления траектории перехода системы в равновесное состояние рассмотрим закрытую систему
металл-шлак (без газовой фазы, без продувки кислородом, кипения металла, поступления материалов и при постоянной температуре). Если скорости перемешивания металла и шлака одинаковы (
), то в этом случае аналитическое решение для состава металла и шлака дает выражение
(7):
 | (6) |
где 
– постоянная
времени.
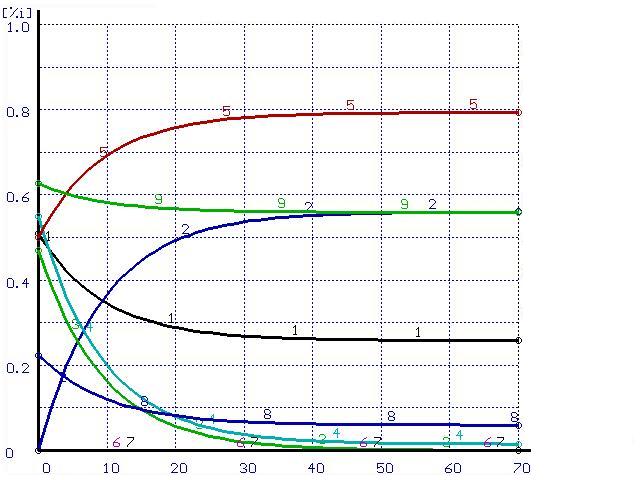
Численный расчет дает аналогичные результаты (см. рис. 1а).
Время, мин |
|
Время, мин |
Рисунок 1. Расчет при 
(а) и при 
(б). Цифры у кривых – содержания элементов в металле и шлаке, масс.%: 1 – 
, 2 – 
, 3 – 
, 4 – 
, 5 – 
[S]*5, 8–
Похожий на (7) результат получается при классическом диффузионном рассмотрении указанного процесса перехода системы в равновесное состояние как диффузионного переноса компонентов под действием градиента концентраций (активностей). Однако в этом случае в формулах (7) в качестве движущей силы фигурирует разность концентраций или активностей, а в качестве коэффициента пропорциональности – коэффициент диффузии, что для реальных агрегатов весьма сомнительно.
В диффузионных уравнениях невозможен переход через равновесное состояние, т.к. у химических элементов нет «инерции» – при достижении равновесной концентрации происходит исчезновение движущей силы. Кроме того, при индивидуальной диффузии не может быть взаимного влияния компонентов и их потоков друг на друга.
Вообще говоря, используемые в кинетике коэффициенты «турбулентной диффузии» – это и есть попытка учесть глобальный массоперенос в рамках классических диффузионных уравнений. Однако отличная от диффузии природа рассматриваемых явлений приводит в некоторых случаях к совершенно иным зависимостям.
Например, экспоненциальное поведение состава металла и шлака наблюдается только при одинаковых скоростях перемешивания металла и шлака, в противном случае возможен временный «переход» содержания некоторых элементов через равновесное состояние (см. рис. 1б).
Интересно, что при этом содержание марганца в первые 7 минут вообще идет в сторону, противоположную конечному равновесному состоянию! Такое поведение марганца легко объясняется сверхравновесным содержанием кремния в этот же интервал времени – пока содержание кремния не снизилось до равновесных значений идет восстановление марганца и фосфора из шлака. После выгорания кремния процесс перехода марганца и фосфора обращается – происходит их снижение до равновесных значений. Возможно, этот эффект и называется в термодинамике необратимых процессов взаимодействием потоков.
Для иллюстрации этого положения был проведен расчет траектории перехода системы в равновесное состояние при импульсном воздействии. В равновесной системе металл-шлак из шлака в металл перенесена некоторая часть кремния. Эти металл и шлак приняты в качестве исходных составляющих системы. Полученные результаты расчетов при различных скоростях перемешивания представлены на рис. 2-3.
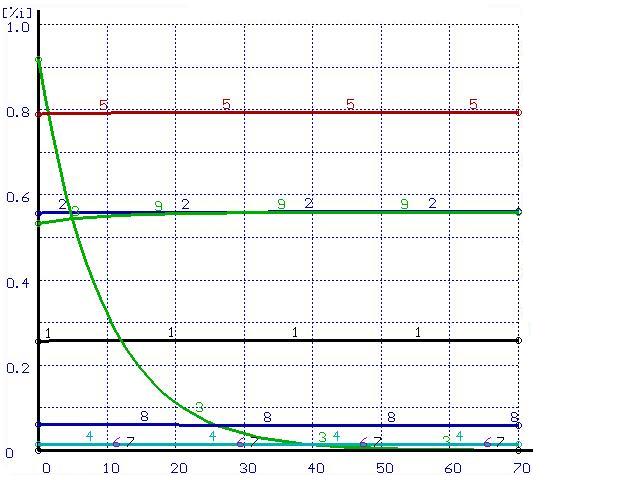
Время, мин |
Рисунок 2. Расчет при 
(обозначения см. на рис. 1)
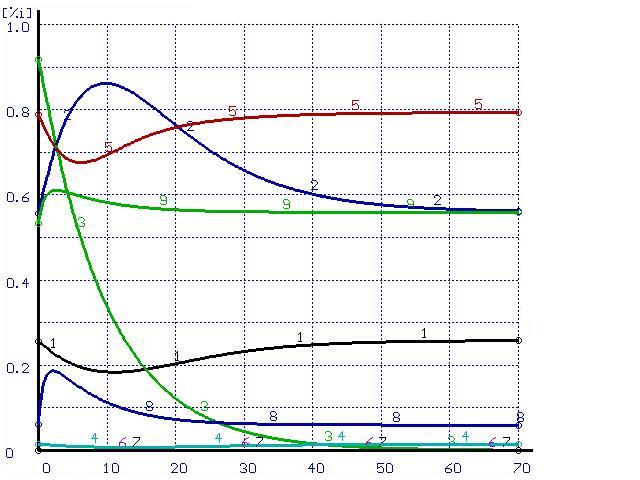
Время, мин |
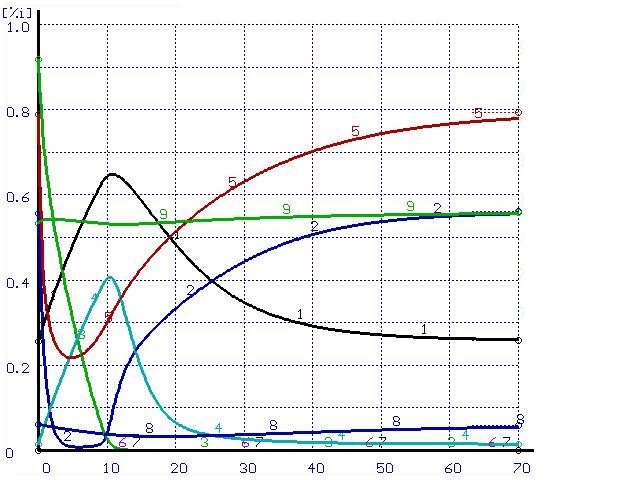
Время, мин |
Рисунок 3. Расчет при 
(а) и при 
(б)
(обозначения см. на рис. 1)
Несмотря на то, что исходный состав системы совпадает с конечным по всем элементам, за исключением кремния, из рисунков видно, что в процессе перехода системы в равновесное состояние под действием потока кремния происходит возникновение потоков всех остальных элементов, составляющих систему. При этом в начальной части всех графиков содержание всех элементов изменяется в сторону, противоположную равновесному состоянию. Возможно, подобные результаты позволят вычислить феноменологические коэффициенты Онзагера.
Аналогичным образом может быть учтен массоперенос при вычислении распределения температуры по глубине ванны.
Аналитическое решение дает для 
(перегрев
поверхности ванны над подиной) и для 
(перегрев
поверхности ванны над средней температурой металла) зависимости вида:
 | (8) | |
 | (9) |
где 
– параметры,
определяемые из геометрии ванны и интенсивности перемешивания.
Например, расчетом получено, что в условиях ММЗ перегрев может достигать 
, 
и более (в зависимости от условий), что подтверждается экспериментами.
Следующий очень важный элемент модели – гидродинамика сталеплавильной ванны, а именно, расчет интенсивности перемешивания. Наиболее ярко и продуктивно его можно проиллюстрировать на примере пульсирующего окисления углерода при кипении сталеплавильной ванны. Нестационарный режим кипения нарушает ход технологического процесса, а иногда бурное вскипание приводит к аварийным выбросам шлака и металла из агрегата. В некоторых случаях окисление углерода происходит только в период пульсаций, что резко снижает технологичность и экономичность процесса плавки. Однозначного объяснения причин такого поведения ванны по ходу плавки пока нет.
В основу расчета положены приведенные ранее принципы, а также уравнение изменения кинетической энергии металла:
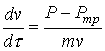 | (10) |
где 
– время, с; 
– скорость
потоков металла, м/c; 
– масса металла, кг; 
, 
– мощность сил трения и перемешивающих сил, Вт;
– мощность перемешивания
металла пузырями оксидов углерода (по формуле Кочо); 
– мощность перемешивания металла струей вдуваемого кислорода.
Исследованиями на основе представленной модели установлено, что произведение 
определяет лишь возможность локального «закипания» ванны металла в печи. Характер и интенсивность процесса по всему объему ванны зависит от скорости движения
потоков жидкого металла, которая определяется следующими факторами: начальным содержанием углерода,
интенсивностью ввода кислорода, интенсивностью внешнего перемешивающего действия, геометрическими параметрами ванны.
Так, при моделировании ДСП-2 БМЗ без донной продувки поведение металла характеризуется резкими периодическими вскипаниями ванны (см. рис. 4). Содержание кислорода в металле в период вскипания несколько снижается, а между пиками концентрация кислорода нарастает до нового толчка. Кривая скорости потоков соответствует кривой интенсивности кипения.
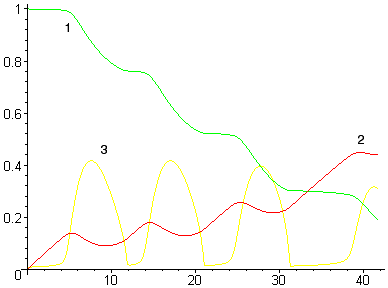
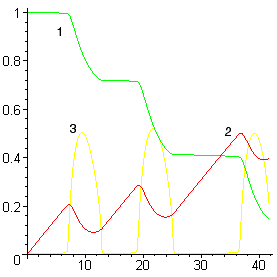
Уменьшение или увеличение интенсивности ввода кислорода (без существенного увеличения мощности перемешивания) принципиально не изменяет качественную картину процесса – ванна периодически вскипает (см. рис. 5а), хотя и с другой периодичностью. Однако при существенном увеличении мощности перемешивания (например, за счет донной продувки инертным газом) кипение переходит в стационарный режим (см. рис. 5б).
Время, мин |
Рисунок 4. Расчет при интенсивности продувки 10 м3/мин.
Цифры у кривых: 1 – 
, 2 – 
, 3 – 
, м/c
Время, мин |
Время, мин |
Рисунок 5. Расчет при низкой (а) и высокой (б)
мощности перемешивания
(обозначения см. на рис. 4)
Рассмотренный подход позволяет полностью описать практически любой металлургический агрегат (ДСП, конвертер, сталеразливочный ковш, установка «печь-ковш», промежуточный ковш и т.д.) на основе декомпозиции протекающих в ванне процессов. Примерная структура математической модели ванны сталеплавильного агрегата может быть следующей:
Все процессы протекают в реакционных зонах (как правило, это границы раздела перечисленных фаз). Важнейшими из них являются: металл–кислород, металл–шлак, металл–футеровка, металл–ферросплавы, шлак–шлакообразующие материалы и др. Алгоритм расчета взаимодействия фаз описан выше.
На основе проведенных исследований построена компьютерная система автоматического проектирования и управления технологическими процессами в условиях БМЗ и ММЗ, которая прошла промышленное опробование, внедрена и дала существенный экономический эффект, выражающийся в стабилизации режима плавки, снижении продолжительности, расхода электроэнергии и металлолома на тонну годного.
|
|
© С.А. Храпко, 2002
| Вверх |
